Solveeit Logo
Login

Question

Question: A car is moving uniformly on a road and a dog suddenly appears at t=0 in front of the car at a dista...

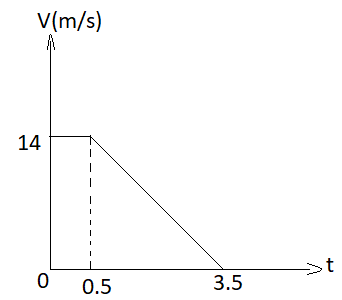
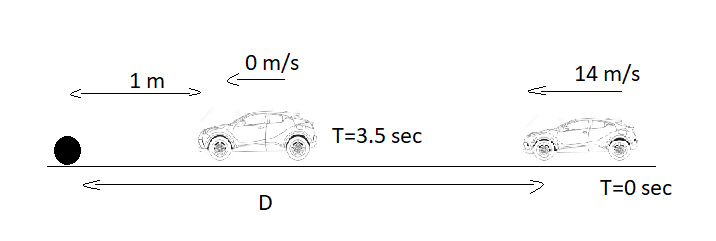
A car is moving uniformly on a road and a dog suddenly appears at t=0 in front of the car at a distance d m. When the driver sees the dog, he brakes the car immediately. The following is the velocity-time graph of the car. The car stops at a distance 1 m from the dog. find d.

Explanation

Solution

To solve this problem first we will calculate distance travelled in first 0.5 sec with initial velocity, after that with the use of third equation of motion we will calculate distance travelled in rest of the time at last we will add both distances and add one to it according to our problem.

Formula used:
Distance =>d=v×t=>d=v\times t
Third equation of motion, =>v2=u2+2as=>{{v}^{2}}={{u}^{2}}+2as

Complete answer:
We can solve our required problem with the basics of one dimensional motion, by using distance time equations and third equations of motion.
Now, for the first 0.5 sec car is moving with the same initial velocity 14 m/s so distance travelled in first 0.5 sec will be given as,

=>d=v×t=>d=v\times t
=>d=14×0.5=7m.........(1)=>d=14\times 0.5=7m.........(1)
Now, for next 3 sec from 0.5 to 3.5 sec the velocity of car drops from 14 m/s to 0 which means final velocity v of car is 0 m/s, and initial velocity is 14 m/s so acceleration of car will be given as,
=>a=ΔvΔt=>a=\dfrac{\Delta v}{\Delta t}
=>a=0−143.5−0.5=−143m/s2=>a=\dfrac{0-14}{3.5-0.5}=\dfrac{-14}{3}m/{{s}^{2}}
Now applying third equation of motion we have,
=>v2=u2+2as=>{{v}^{2}}={{u}^{2}}+2as
=>02=142+2×(−143)×s=>{{0}^{2}}={{14}^{2}}+2\times \left( -\dfrac{14}{3} \right)\times s
=>283×s=142=>\dfrac{28}{3}\times s={{14}^{2}}
=>s=21m............(2)=>s=21m............(2)
Now according to the question car stops 1 m before the dog so by adding eqn (1), (2) and adding 1 in it we will get our required answer so,
=>D=7+21+1=29m=>D=7+21+1=29m
∴\therefore The distance d between dog and car before applying brakes is 29m.

Note:
In the above solution we can observe that acceleration is constant and negative (car is slowing down with time) or we can directly deduce from the graph itself as velocity-time graph slope is straight line and negative. So we can apply a third equation of motion which can only work for constant acceleration.