Question

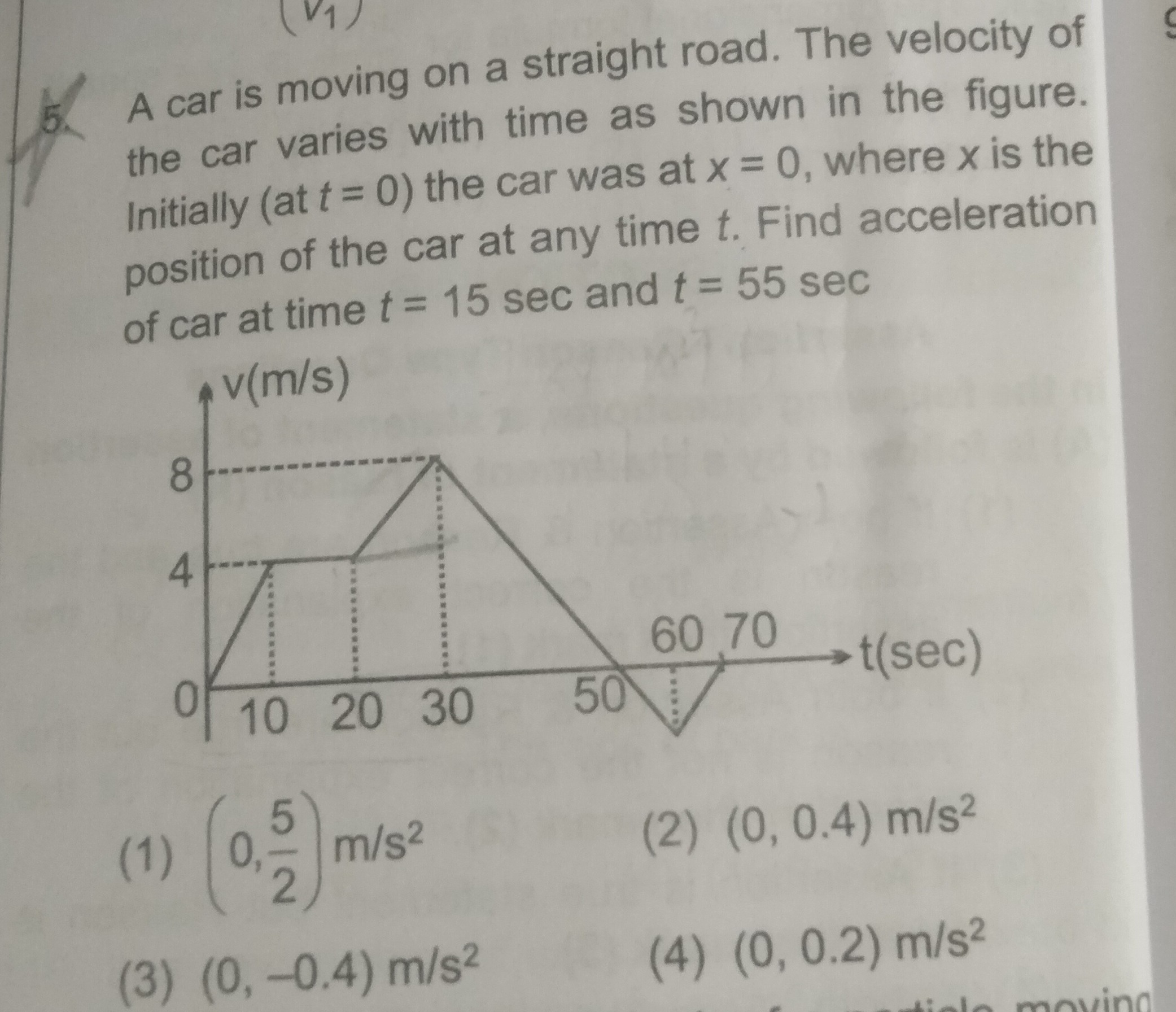
A car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t = 0) the car was at x = 0, where x is the position of the car at any time t. Find acceleration of car at time t = 15 sec and t = 55 sec

• A. $\left(0,\frac{5}{2}\right) m/s^2$
• B. (0, 0.4) m/s²
• C. (0, -0.4) m/s²
• D. (0, 0.2) m/s²

Answer 1

Answer: (C)

(0, -0.4) m/s²

Answer 2

The acceleration of the car at any time 't' is given by the slope of the velocity-time (v-t) graph at that instant.

At t = 15 sec:

The graph segment between t = 10 sec and t = 20 sec is a horizontal line, indicating constant velocity.

Velocity at t = 10 sec is 4 m/s.

Velocity at t = 20 sec is 4 m/s.

Acceleration ($a_{15}$) = Slope = $\frac{\Delta v}{\Delta t} = \frac{4 - 4}{20 - 10} = \frac{0}{10} = 0 \, \text{m/s}^2$.

At t = 55 sec:

The graph segment between t = 50 sec and t = 60 sec is a straight line.

Velocity at t = 50 sec is 0 m/s.

Velocity at t = 60 sec is -4 m/s.

Acceleration ($a_{55}$) = Slope = $\frac{\Delta v}{\Delta t} = \frac{-4 - 0}{60 - 50} = \frac{-4}{10} = -0.4 \, \text{m/s}^2$.

Thus, the accelerations are (0, -0.4) m/s².