Question

A car is moving on a circular level road of curvature 300m. If the coefficient of friction is 0.3 and acceleration due to gravity is $10m/{{s}^{2}}$, the maximum speed of the car be
A. 30km/h
B. 81km/h
C. 108 km/h
D. 162 km/h

Answer 1

Use the concept of banking of road. Try to resolve the forces on the car. Gravitational force and normal force will definitely be on the car which is balancing each other. In this question, if a car is slipping away from the road then centrifugal force must be acting on the body. We know that maximum speed is given by following formula ${{v}_{\max }}=\sqrt{Rg\left[ \dfrac{{{\mu }_{s}}+\tan \theta }{1-{{\mu }_{s}}\tan \theta } \right]}$, and we also know that for curved horizontal road, angle of banking is zero. Put the value in the above equation, you will get ${{v}_{\max }}$.

Complete step-by-step answer:

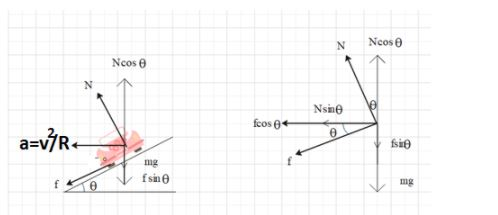
$mg=\text{ weight of vehicle}$
$N=\text{Normal reaction}$
$f=\text{frictional force}$
$a=\dfrac{{{v}^{2}}}{R}-\text{centripetal acceleration}$

& f\cos \theta =\text{horizontal component of frictional force}\text{.} \\\ & f\sin \theta =\text{vertical component of frictional force}\text{.} \\\ & \text{Ncos}\theta =\text{ vertical component of normal reaction}\text{.} \\\ & \text{Nsin}\theta \text{= horizontal component of normal reaction}\text{.} \\\ \end{aligned}$$ Consider a vehicle of mass $m$ moving with velocity $v$ along a curved banked road banked at an angle. Let $f$ be the frictional force between tyres of the vehicle and road surface. The forces acting on vehicle are, (1) Weight mg acting vertically downward (2) Normal reaction $$N$$ in upward direction though centre of gravity and perpendicular to banked road/surface. The frictional force between tyres of vehicle and road surface can be resolved into $\begin{aligned} & f\cos \theta =\text{along horizontal direction} \\\ & f\sin \theta =\text{along vertical downward direction} \\\ \end{aligned}$ The normal reaction can be resolved into two components, $\begin{aligned} & N\cos \theta =\text{vertical component of normal reaction}\text{.} \\\ & \text{Nsin}\theta \text{= horizontal component of normal reaction}\text{.} \\\ \end{aligned}$ The component $N\cos \theta $of normal reaction is balanced by weight $$mg$$of vehicle and component $f\sin \theta $ of frictional force, $\begin{aligned} & N\cos \theta =mg+f\sin \theta \\\ & \therefore mg=N\cos \theta -f\sin \theta ----(1) \\\ \end{aligned}$ Horizontal component $N\sin \theta $ along with the component of $f\cos \theta $ of frictional force provides the necessary centripetal force. $\begin{aligned} & N\sin \theta +f\sin \theta =\dfrac{m{{v}^{2}}}{R} \\\ & \dfrac{m{{v}^{2}}}{R}=N\sin \theta +f\sin \theta -----(2) \\\ \end{aligned}$ Dividing (1) by (2), we get $\dfrac{{{v}^{2}}}{Rg}=\dfrac{N\sin \theta -f\cos \theta }{N\cos \theta -f\sin \theta }$ The magnitude of frictional force depends on the speed of the vehicle for the given road surface and tyres of the vehicle. Let ${{v}_{\max }}$denote maximum speed of vehicle, the frictional force ${{f}_{m}}$ produced at this speed should be ${{f}_{m}}={{\mu }_{s}}N$ $\dfrac{{{v}^{2}}_{\max }}{Rg}=\dfrac{N\sin \theta -{{f}_{m}}\cos \theta }{N\cos \theta -{{f}_{m}}\sin \theta }$ $\therefore {{v}_{\max }}=\sqrt{Rg\left[ \dfrac{{{\mu }_{s}}+\tan \theta }{1-{{\mu }_{s}}\tan \theta } \right]}$ For a curved horizontal road$\theta ={{0}^{0}}$, hence above equation becomes ${{v}_{\max }}=\sqrt{\mu Rg}$  Aim- When a car is turning from the circular road then a car will sleep if it exceeds maximum speed. Find its maximum speed. Force acting on the car are: Force acting downward on the car which is mg To balance this force, a normal force acts i.e. N Outside of the car, force acting is centrifugal force F And to balance this centrifugal force, a frictional force is acting toward the road as shown in the diagram. So from this above statement, we can write as N=mg -------(1) And $f=\mu N=\mu mg................(2)$ We know that centrifugal force is the force acting away from the centre of the body when the body does circular motion and it is given as, $F=\dfrac{m{{v}^{2}}}{r}.....................(3)$ To balance the car and make a smooth turn while running the car on a curved road, frictional force must be equal to centripetal force. From equation (1) and (2), $\dfrac{m{{v}^{2}}}{r}=\mu mg$ Cancel m from both sides. We get, ${{v}_{\max }}=\sqrt{\mu gr}=\sqrt{0.3\times 10\times 300}=30m/s$ The calculated value of velocity is in m/s but our options are in km/s. So convert m/s into km/s. ${{v}_{\max }}=30m/s\times \dfrac{18}{5}=108km/hr$ A maximum speed of car can be $108km/hr$ **So, the correct answer is “Option C”.** **Note:** Do not get confused between centripetal force and Centrifugal force. Centrifugal force is the force acting away from the centre of the body when the body does circular motion. Centripetal force is the force acting towards the centre of the body when the body does circular motion. Look for units. Once calculation has been done, check options in which unit it is given. Convert it accordingly. To convert m/s into km/s, multiply answer by 18 and divide it by 5.