Question

A car is moving along a hilly road as shown (side view). The coefficient of static friction between the tyres and the pavement is constant and the car maintains a steady speed. If at one of the points shown the driver applies brakes as hard as possible without slipping, the magnitude of the frictional force immediately after the brakes are applied will be maximum if the car was at:

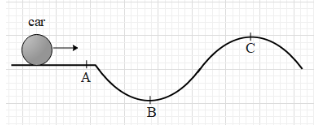
A. Point A
B. Point B
C. Point C
D. Friction force is the same at all three points.

Answer 1

It is given that the coefficient of friction is constant everywhere. Then this means that the frictional force is maximum where the normal reaction is maximum. Find the normal forces when the car is at each of the points.

Formula used:
$f=\mu N$, where f is the friction on a body moving on a surface with coefficient of friction $\mu$ and normal force N exerted by the surface.
${{F}_{g}}=mg$, where ${{F}_{g}}$ is the gravitational force on a body of mass m and g is acceleration due to gravity.
$F=\dfrac{m{{v}^{2}}}{r}$, where F is the centripetal force on a body moving in a circular motion of radius r with velocity v.

Complete step by step answer:
The static frictional force on the car is given as $f=\mu N$. It is given that the coefficient of friction is constant everywhere. Then this means that the frictional force is maximum where the normal reaction is maximum.Let us find the normal reaction (N) on the car exerted by the ground at all the three points. Let the mass of the car be M.
At point A:
Here, we can see that the car is moving on a horizontal surface. The gravitational force exerted by the earth is in the downward direction (perpendicular to the ground surface). We know that the car is not accelerating in the vertical direction. Therefore, the acceleration in the vertical direction is zero.

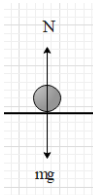
This means that the gravitational force is balanced by the normal reaction force exerted by the ground.
i.e. $N=mg$ …. (i)
Therefore, the friction force at point A is ${{f}_{A}}=\mu mg$
At point B:
Here, the car is moving on a curved path. Let the radius of curvature of the surface at point B be r. Due to the curved path, the car will have a centripetal force which is equal to $F=\dfrac{m{{v}^{2}}}{r}$. The direction of this force is upward direction.

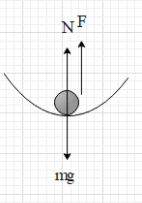
Therefore, the net force acting on the car in the vertical direction at this point is ${{F}_{net}}=\dfrac{m{{v}^{2}}}{r}+N-mg$.
But ${{F}_{net}}=0$
$\Rightarrow \dfrac{m{{v}^{2}}}{r}+N-mg=0$
$\Rightarrow N=mg-\dfrac{m{{v}^{2}}}{r}$ ….. (ii)
At point C:
Let us assume that the radius of curvature of the surface at point C is r. Then the centripetal force on the car at this point is $F=\dfrac{m{{v}^{2}}}{r}$ but in the downward direction.

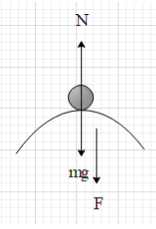
Therefore, the net force on the car in the vertical direction at this point is ${{F}_{net}}=N-mg-\dfrac{m{{v}^{2}}}{r}$
But we know that ${{F}_{net}}=0$.
$\Rightarrow N=mg+\dfrac{m{{v}^{2}}}{r}$ ….. (iii)
Now, when we compare (i), (ii) and (iii) we get that the value of N is maximum at point C.This means that maximum friction is at point C.

Hence, the answer is C.

Note: One may argue that why we assumed that radius of the curvature at point C to be r, which is the same as that of at point B. We assumed that because it does not matter whether we consider it same or different than that of at point B. If we see (ii) and (iii), we get that some value is added or subtracted from constant term mg. Therefore, irrespective of the value of the two radii of curvature, the value of N is less in (ii) than that of in (iii).