Question

A car is going from one city by travelling $75km$ North, $60\sqrt 2 km$ North-West and $60km$ East. The minimum distance between the two cities is:
A) $135km$.
B) $137km$.
C) $140km$.
D) $170km$.

Answer 1

A vector quantity is the quantity which has magnitude as well as direction. The displacement is defined as the shortest distance between initial and final point of the motion. The magnitude of the vector can be calculated by applying the difference of the final and initial coordinates and taking the sum of squares of the resultant.

Formula used:
The formula of the resultant of the vector $a\hat i + b\hat j$ is given by,
$R = \sqrt {{a^2} + {b^2}}$.
Where R is the resultant the coefficient of the x-axis is a and the coefficient of y-direction is b.

Complete step by step solution:
It is given the problem that a car is going from one city by travelling $75km$ North, $60\sqrt 2 km$ North-West and $60km$ East and we need to find the minimum distance between the two cities.

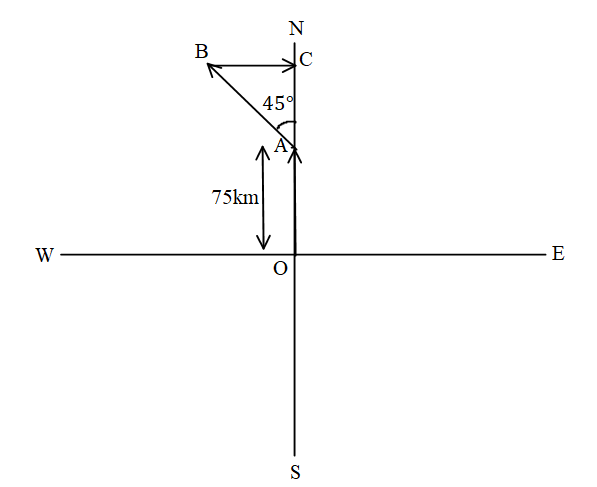
The displacement of the car is equal to,
$\Rightarrow d = 75\hat j - 60\sqrt 2 \cos 45^\circ \hat i + 60\sqrt 2 \sin 45^\circ \hat j + 60\hat i$
$\Rightarrow d = 75\hat j - 60 \cdot \sqrt 2 \left( {\dfrac{1}{{\sqrt 2 }}} \right)\hat i + 60 \cdot \sqrt 2 \left( {\dfrac{1}{{\sqrt 2 }}} \right)\hat j + 60\hat i$
$\Rightarrow d = 75\hat j - 60\hat i + 60\hat j + 60\hat i$
$\Rightarrow d = 75\hat j + 60\hat j$
$\Rightarrow d = 135\hat j$

The displacement of the car is equal to 135km. The correct answer for this problem is option (A).

Note: The distance is the total path travelled by the body and the displacement is the shortest path between the initial and final position of the body. The $\hat i$ is the representation of the x-direction and the $\hat j$ is the representation of the y-axis.