Question

A car is going at a speed of $21.6\,km \cdot h{r^{ - 1}}$ when it encounters a $12.8\,m$ long slope of angle ${30^ \circ }$. The friction coefficient between the road and the tyre is $\dfrac{1}{{2\sqrt 3 }}$. Show that no matter how hard the driver applies the brakes, the car will reach the bottom with a speed greater than $36\,km \cdot h{r^{ - 1}}$.

Answer 1

To solve this problem, find the equation of motion of the car when it is dropping from the slope from the equation of motion while considering the brake and find the velocity of the car at the end of the slope.

Formula used:
Newton’s second law of motion is given by,
${F_{net}} = Ma$
where, ${F_{net}}$ is the net force acting on the body of mass $M$ and $a$ is the acceleration of the body.
The frictional force acting on a body is given by,
$f = \mu N$
where, $\mu$ is the coefficient of friction and$N$ is the normal force by the surface.
The equation for one dimensional motion is given by,
${v^2} = {u^2} + 2as$
where $v$ is the velocity of the body , $a$ is the acceleration of the body, $s$ is the displacement of the body and $u$ is the initial velocity of the body.

Complete step by step answer:
We have given here a car which is moving with a velocity of $21.6\,km \cdot h{r^{ - 1}}$ and counters a $12.8\,m$ slope. The coefficient of friction between the road and the tyre is $\dfrac{1}{{2\sqrt 3 }}$. Now, we have to find the speed of the car at the end of the slope.Now, if the car brakes the maximum force that can be applied by brake is the frictional force between the road and the tyre. Now, the gravitational force is acting vertically downward.So, the component of gravitational acceleration that will act along the slope is $g\sin \theta$.

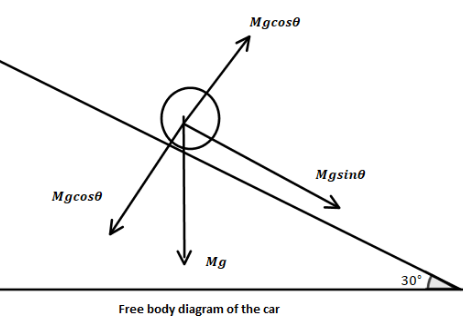
So, the equation of motion letting the mass of the car $M$with maximum braking can be written as,
$Mg\sin \theta - \mu Mg\cos \theta = Ma$
$\Rightarrow a = g\sin \theta - \mu g\cos \theta$
$\Rightarrow a = g(\sin \theta - \mu \cos \theta )$
So, putting the values we will have,
$a = 10(\sin {30^ \circ } - \dfrac{1}{{2\sqrt 3 }}\cos {30^ \circ })$
$\Rightarrow a = 10(\dfrac{1}{2} - \dfrac{1}{{2\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{2})$
$\Rightarrow a = 10(\dfrac{1}{2} - \dfrac{1}{4})$
$\Rightarrow a = \dfrac{{10}}{4}$
$\Rightarrow a = 2.5$
So, the car will still have an acceleration of $2.5\,m{s^{ - 2}}$ with even maximum braking.

Now, the initial speed of the car is $21.6\,km \cdot h{r^{ - 1}}$

\Rightarrow u = 6\,m{s^{ - 1}}$$ The length of the slope is $$12.8\,m$$.Hence, using the relation $${v^2} = {u^2} + 2as$$. We have, $${v^2} = {6^2} + 2 \times 2.5 \times 12.8$$ $$\Rightarrow {v^2} = 100$$ $$\therefore v = 10$$ So, the car will have a minimum velocity of $$10\,m{s^{ - 1}}$$ or $$\dfrac{{10 \times 3600}}{{1000}} = 36\,km \cdot h{r^{ - 1}}$$. **Hence, it is proved that even with maximum braking the car will still have a minimum velocity of $$36\,km \cdot h{r^{ - 1}}$$ at the end of the slope.** **Note:** The brake applied by the car is only equal to the frictional force due to the surface if the car applied reverse acceleration then the car can be stopped more easily with applied force greater or equal to the net acceleration the car is subjected to stop in between the slope or can move with uniform velocity. But to do so the car needs to apply energy meaning needed engine power equal to the mass times acceleration.