Question

A car covers $30\,{\text{km}}$ at a uniform speed of $60\,{\text{km}}{{\text{h}}^{ - 1}}$ and the next $30\,{\text{km}}$ at a uniform speed of $40\,{\text{km}}{{\text{h}}^{ - 1}}$. Find the total time taken.
A. $30\,\min$
B. $45\,\min$
C. $75\,\min$
D. $120\,\min$

Answer 1

We are asked to find the total time taken by a car to travel the total distance of $60\,{\text{km}}$. As, the speed is different for the first $30\,{\text{km}}$ and next $30\,{\text{km}}$, so find the time taken for each part separately and add them to find the total time taken. You will need to use the formula for time taken in terms of distance and speed.

Complete step by step answer:
Given, a car covers a distance $30\,{\text{km}}$ at a uniform speed of $60\,{\text{km}}{{\text{h}}^{ - 1}}$.
And covers next $30\,{\text{km}}$ at a uniform speed of $40\,{\text{km}}{{\text{h}}^{ - 1}}$.
The formula we will use to calculate the time taken is,
${\text{time}}\,{\text{taken}} = \dfrac{{{\text{Distance}}}}{{{\text{Speed}}}}$ ……………(i)
Let us draw a rough diagram to understand the problem properly.

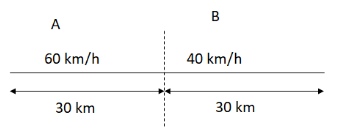
We have divided the problem into two parts, part A and part B.
In part A, the car covers distance, ${d_A} = 30\,{\text{km}}$ with uniform speed, ${v_A} = 60\,{\text{km}}{{\text{h}}^{ - 1}}$
In part B, the car covers distance, ${d_B} = 30\,{\text{km}}$ with uniform speed, ${v_B} = 40\,{\text{km}}{{\text{h}}^{ - 1}}$

Now, we will find the time taken for part A and part B separately and then add them to find the total time taken.For part A, using the formula from equation (i) we get the time taken as,
${t_A} = \dfrac{{{d_A}}}{{{v_A}}}$
Putting the values of ${d_A}$ and ${v_A}$, we get,
${t_A} = \dfrac{{30\,{\text{km}}}}{{60\,{\text{km}}{{\text{h}}^{{\text{ - 1}}}}}}$
$\Rightarrow {t_A} = \dfrac{1}{2}{\text{hr}}$
$\Rightarrow {t_A} = 0.5{\text{hr}}$ ………………(ii)

For part B using the formula from equation (i), we get the time taken as,
${t_B} = \dfrac{{{d_B}}}{{{v_B}}}$
Putting the values of ${d_B}$ and ${v_B}$, we get
${t_B} = \dfrac{{30\,{\text{km}}}}{{40\,{\text{km}}{{\text{h}}^{{\text{ - 1}}}}}}$
$\Rightarrow {t_B} = \dfrac{3}{4}{\text{hr}}$
$\Rightarrow {t_B} = 0.75{\text{hr}}$ …………………(iii)
Therefore, we will get the total time taken by adding the time taken in part A and time taken in part B.
$\therefore {t_{total}} = {t_A} + {t_B}$
Putting the values of ${t_A}$ and ${t_B}$, we get
${t_{total}} = 0.5\,{\text{hr}} + 0.75\,{\text{hr}}$
$\Rightarrow {t_{total}} = 1.25\,{\text{hr}}$
The options are given in minutes, so we convert hours to minutes.
${t_{total}} = 1.25\, \times 60\,\min$
$\therefore {t_{total}} = 75\,\min$
Therefore, total time taken is $75\,\min$.

Hence, the correct answer is option C.

Note: Remember whenever speeds are different for the same distance travelled, the time taken will also be different. If in the given question the speeds for part A and part B were the same, then we could calculate the total time taken using the total distance covered and the speed without calculating for each part separately.