Question

A car approaching a crossing at a speed of $20m/s$sounds a horn of frequency $628Hz$when $80m$from the crossing. The apparent frequency heard by an observer $60m$from the crossing on the straight road which crosses the road at right angle is (velocity of sound$= 330m/s$)
(A) $660HZ$
(B) $680HZ$
(C) $640HZ$
(D) $690HZ$

Answer 1

To solve this question,we have to apply the concept of Doppler effect in sound.

Complete step by step answer:
According to the Doppler Effect in sound, the frequency of sound changes with the relative motions of the source and observer. This change in frequency is called apparent frequency.

Apparent frequency is given by the formula
$f' = \dfrac{{(v - {v_0})}}{{(v - {v_s})}}f$
Where $f'$is the apparent frequency of the sound?
$f$is the real frequency.
$v$is the velocity of sound , velocity of sound$= 330m/s$.
${v_0}$is the velocity of the observer.
${v_s}$is the velocity of the source.
Here, the source is a moving car. Car’s velocity is denoted as ${v_s}'$ because the observer and path of the car are in a right angle way.
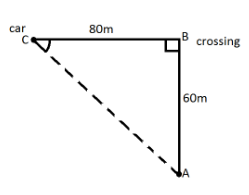
But this observer and the source are at right angles to each other, as shown in the figure.
Only the cosine component of the car’s velocity is contributed in this equation of Doppler shift. Because car velocity's cosine component is parallel to the direction of the observer.
From the figure $\tan \theta = AB/BC = \dfrac{{60}}{{80}} = 0.75$
This angle between the car’s velocity direction and the direction towards the observer from the point $C$.
$\theta = {\tan ^{ - 1}}(0.75) = {36.87^0}$
${v_s} = {v_s}'\cos \theta = 20\cos (36.87) = 16m/s$
Since the observer is at rest ${v_o}$is zero.

f' = \dfrac{{(v - {v_0})}}{{(v - {v_s})}}f = (\dfrac{{330}}{{330 - 16}}) \times 628 = 660Hz \\\ \end{gathered} $$ So the answer is (A)$$660HZ$$ **Note:** Doppler Effect is present in all kinds of waves, including sound waves, electromagnetic waves, etc.This effect is we can see in daily life, like changing in pitch sound of approaching train, supersonic jet, etc.The apparent frequency depends on whether the source is approaches or receding.Doppler Effect has several applications like medical imaging, radars, and more predominantly in astronomy.Velocity of sound in the outer space is zero because sound waves need a medium.