Question

A car $A$ is travelling on a straight level road with a speed of $60km{h^{ - 1}}$ . It is followed by another car $B$ which is moving with a speed of $70km{h^{ - 1}}$ . When the distance between them is $2.5km$ , the car $B$ is given a deceleration of $20km{h^{ - 2}}$ .After what distance and time will the car $B$ catch up car $A$

Answer 1

In this problem the two cars moves in the same direction with the velocity $60km{h^{ - 1}}$ and $70km{h^{ - 1}}$ respectively as shown in the figure below and the deceleration of the car $B$ is given as $20km{h^{ - 2}}$ we need to use the formula $s = ut + \dfrac{1}{2}a{t^2}$ to find the acceleration and time.

Complete step-by-step solution:

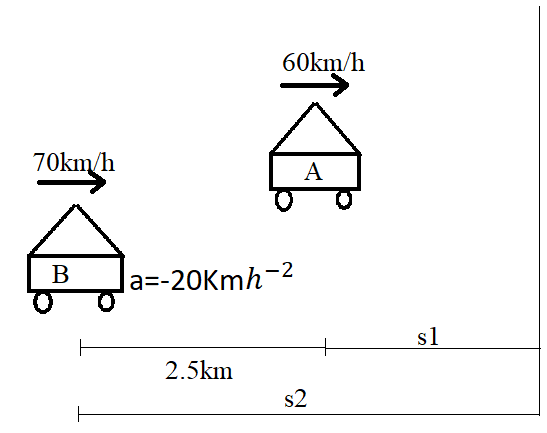
Given
Speed of car $A = 60km{h^{ - 1}}$
Speed of car $B = 70km{h^{ - 1}}$
Distance between car $B$ and $A = 2.5km$
deceleration, $a = - 20km{h^{ - 2}}$
For car $A$
${s_1} = ut = 60t$ ………..$\left( 1 \right)$
For car $B$
${s_2} = ut + \dfrac{1}{2}a{t^2}$
Substituting the given value we get
${s_2} = 70t + \dfrac{1}{2}\left( { - 20} \right){t^2}$
${s_2} = 70t - 10{t^2}$ …………$\left( 2 \right)$
From the diagram it is clear that $2.5 = {s_2} - {s_1}$ ……….$\left( 3 \right)$
Substituting equation $\left( 1 \right)$ and equation $\left( 2 \right)$ in equation $\left( 3 \right)$
$2.5 = 70t - 10{t^2} - 60t$
On simplifying
$10{t^2} - 10t + 2.5 = 0$
On factorization the above equation we get
$t = 0.5h$
Substituting in equation $\left( 2 \right)$
${s_2} = 70\left( {0.5} \right) - 10{\left( {0.5} \right)^2}$
${s_2} = 32.5km$
Hence the distance is $32.5km$ and time is $t = 0.5h$

Note: Since the speed of two cars are given in terms of $km{h^{ - 1}}$ and distance in $km$ we can do calculations by considering the same unit and after calculation we will get time $h$ and distance in $km$ .