Question

A car A is going northeast at 80 km/h and another car B is going southeast at 60 km/h. then the direction of the velocity of A relative to V makes with the north an angle $a$ such that $\tan a$ is:
(A) $\dfrac{1}{7}$
(B) $\dfrac{{\sqrt 2 }}{7}$
(C) $\dfrac{{\sqrt 7 }}{2}$
(D) $1$

Answer 1

The velocity of car A relative to car B is graphically the arrow drawn from the tip of the arrow representing the velocity of car B to the tip of the arrow representing the velocity of car A. The angle between the direction of car A and car B is 90 degrees.
Formula used: In this solution we will be using the following formulae;

Complete Step-by-Step Solution:

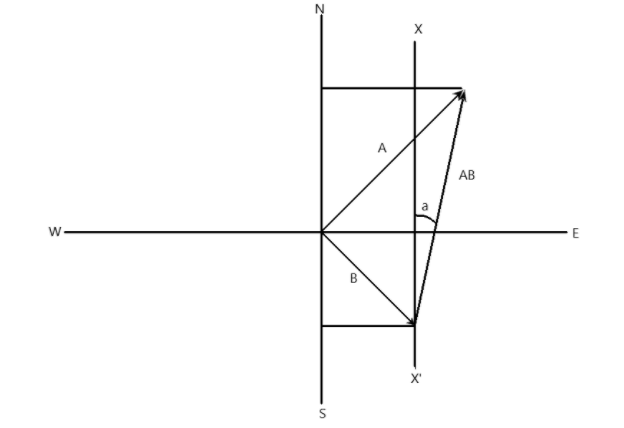
To find the angle, we can draw a graphical representation of the situation stated in the question as shown above.
The velocity of A with respect to B is shown by the arrow joining the tip of the velocity of car B to the tip of velocity of car A as seen in figure. Since car A is northeast and car B is southeast, the angle between them is hence 90 degrees, and hence 45 degree angle is between them and both axes (north and east). Hence, the three vectors make up a right angled triangle.
We can see from observation, that the component of AB on the north axis is the sum of the component of B and A on the same north axis. Hence,
${V_{AB}}\cos a = 80\cos 45^\circ + 60\cos 45^\circ$
$\Rightarrow {V_{AB}}\cos a = 80\dfrac{{\sqrt 2 }}{2} + 60\dfrac{{\sqrt 2 }}{2} = 10\left( {4\sqrt 2 + 3\sqrt 2 } \right)$
Also, the component on the east axis (horizontal) is the component of A on the horizontal minus the component of B on the horizontal, hence,
${V_{AB}}\sin a = 80\sin 45^\circ - 60\cos 45^\circ$
$\Rightarrow {V_{AB}}\sin a = 80\dfrac{{\sqrt 2 }}{2} - 60\dfrac{{\sqrt 2 }}{2} = 10\left( {4\sqrt 2 - 3\sqrt 2 } \right)$
By dividing the vertical and horizontal component, we get
$\dfrac{{{V_{AB}}\sin a}}{{{V_{AB}}\cos a}} = \dfrac{{10\left( {4\sqrt 2 - 3\sqrt 2 } \right)}}{{10\left( {4\sqrt 2 - 3\sqrt 2 } \right)}} = \dfrac{{\left( {4\sqrt 2 - 3\sqrt 2 } \right)}}{{\left( {4\sqrt 2 + 3\sqrt 2 } \right)}}$
$\Rightarrow \tan a = \dfrac{{\left( {4\sqrt 2 - 3\sqrt 2 } \right)}}{{\left( {4\sqrt 2 + 3\sqrt 2 } \right)}}$
$\Rightarrow \tan a = \dfrac{{\sqrt 2 }}{{7\sqrt 2 }} = \dfrac{1}{7}$

Hence, the correct option is A

Note: for clarity, the angle $a$ is the angle the velocity makes with the north axis because by mathematical principles the angle a line A makes with another line B is equal the angle the line A will make with another line C which is parallel to the line B. the line XX’ is parallel to the north axis.