Question

A capillary tube is dipped in liquid. Let pressures at points $A,B$ and $C$ be ${P_A},{P_B}$ and ${P_C}$ respectively, then

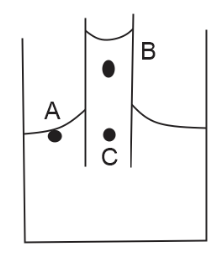
(A) ${P_A} = {P_B} = {P_C}$
(B) ${P_A} = {P_B} < {P_C}$
(C) ${P_A} = {P_C} < {P_B}$
(D) ${P_A} = {P_C} > {P_B}$

Answer 1

It is a logic based question using the concept that pressure exerted on molecules reduces with their depth inside the liquid.

Complete step by step answer:

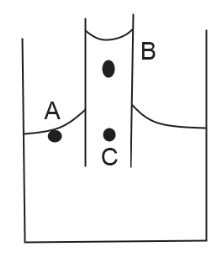
It is given that ${P_A}$ is the pressure at point.
${P_B}$ is the pressure at point $B$.
${P_C}$ is the pressure at point $C$.
We can observe in the diagram that both$A$and$C$are in the same liquid and at the same level.
Therefore, clearly, pressure exerted on the both of them will also be equal.
$\Rightarrow {P_A} = {P_C}$ . . . (1)
Therefore, option (B).${P_A} = {P_B} < {P_C}$ is incorrect.
Now, we know that the pressure exerted by a column of liquid at any point on liquid surface given by
$P = egh$ . . . (2)
Where, $P$ is pressure exerted at a point.
$e$ is the density of liquid.
$h$ is the height of the liquid column.
$g$ is acceleration due to gravity.
Now, let us assume that the height between $B$ and $C$ is $h$.
Then, using equation (1), we can write
$\Rightarrow {P_B} = {P_C} + egh$
($\because B$ is above $C$)
Therefore, clearly pressure exerted on $B$ is greater than $C$
$\Rightarrow {P_B} > {P_C}$ . . . (3)
Therefore, from equation (1) and (3),
We can write
$\Rightarrow {P_A} = {P_C} < {P_B}$
Therefore, from the above explanation the correct option is (C).${P_A} = {P_C} < {P_B}$.

Note: The pressure is exerted by the atmosphere, the pressure on the molecules on the surface of liquid is more than the molecules which are in depth, inside the liquid.