Question

A capacitor with circular plates of radius R is charged with a constant current I as shown. Which of the following are correct?

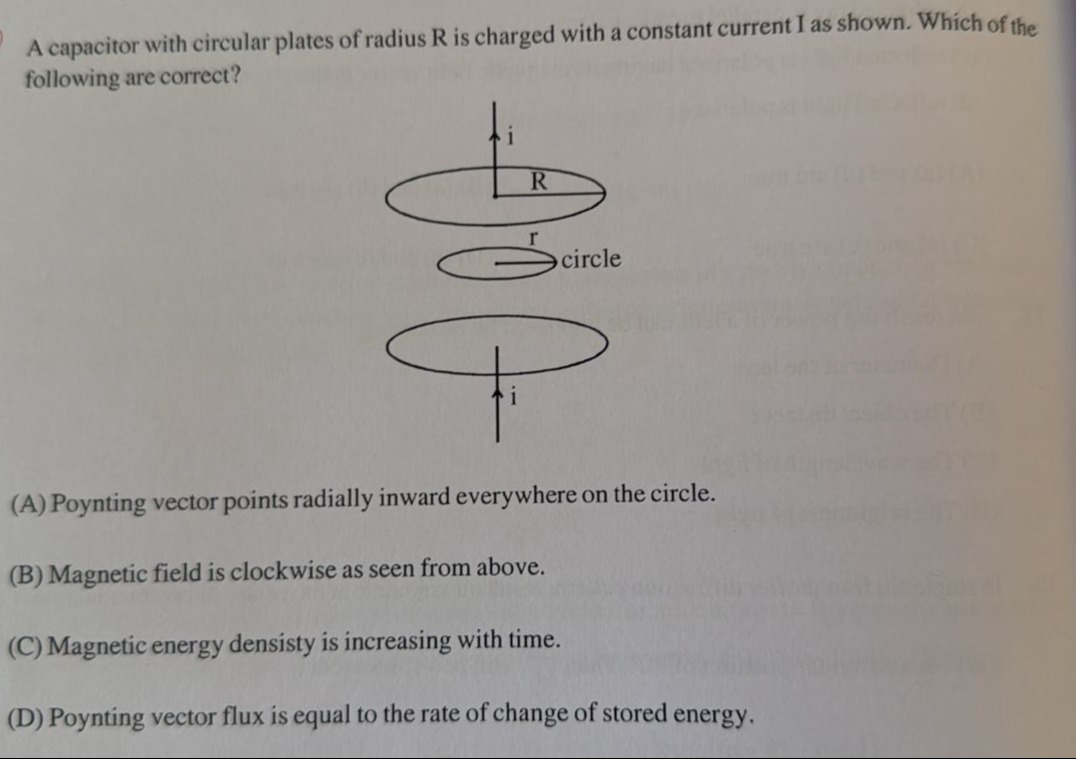
• A. Poynting vector points radially inward everywhere on the circle.
• B. Magnetic field is clockwise as seen from above.
• C. Magnetic energy densisty is increasing with time.
• D. Poynting vector flux is equal to the rate of change of stored energy.

Answer 1

Answer: (A), (B), (D)

(A), (B), (D)

Answer 2

The given question is about a parallel plate capacitor being charged by a constant current. We need to analyze the properties of the electromagnetic fields and energy in the region between the plates.

(A) Poynting vector points radially inward everywhere on the circle.

The electric field between the plates points from the positive plate to the negative plate. Assuming the current I enters the top plate, it becomes positively charged, and the bottom plate becomes negatively charged. So, the electric field $\vec{E}$ points downwards. The charging current creates a displacement current between the plates, which acts as a source for the magnetic field. Using Ampere-Maxwell's law, the magnetic field $\vec{B}$ between the plates is found to be tangential and forms circles around the central axis. Using the right-hand rule with the downward displacement current, the magnetic field is clockwise as seen from above. The Poynting vector is given by $\vec{S} = \frac{1}{\mu_0} (\vec{E} \times \vec{B})$. If $\vec{E}$ is downwards and $\vec{B}$ is tangential (clockwise when viewed from above), then $\vec{E} \times \vec{B}$ points radially inward. Thus, the Poynting vector points radially inward. So, option (A) is correct.

(B) Magnetic field is clockwise as seen from above.

As explained in (A), the magnetic field is clockwise as seen from above. So, option (B) is correct.

(C) Magnetic energy density is increasing with time.

The magnetic field between the plates at a distance $r$ from the axis ($r \le R$) is given by $B = \frac{\mu_0 I r}{2\pi R^2}$. Since the charging current I is constant, the magnetic field B at any point is constant in time. The magnetic energy density is $u_B = \frac{B^2}{2\mu_0}$. Since B is constant, $u_B$ is also constant in time. So, option (C) is incorrect.

(D) Poynting vector flux is equal to the rate of change of stored energy.

According to Poynting's theorem, for a volume V, $\oint_S \vec{S} \cdot d\vec{A} = -\frac{d}{dt}(U_E + U_B) - P_{dissipated}$, where the integral is over the surface S enclosing V, $U_E$ is the electric energy stored, $U_B$ is the magnetic energy stored, and $P_{dissipated}$ is the power dissipated within the volume. The integral represents the power flowing out of the volume. If the integral is taken with the area vector pointing inward, then $-\oint_S \vec{S} \cdot d\vec{A}$ represents the power flowing into the volume. In the region between the capacitor plates, there is no conduction current, so the power dissipated is zero. Thus, the net power flowing into the region is equal to the rate of increase of the total stored energy. The Poynting vector points radially inward, so the flux of the Poynting vector into the region between the plates through the cylindrical surface at $r=R$ (between the plates) represents the rate at which energy is flowing into this region. The Poynting vector flux mentioned in option (D) is likely referring to the total flux into the volume, which is equal to the rate of change of stored energy. The rate of change of stored energy is $\frac{d}{dt}(U_E + U_B)$. We found that $U_B$ is constant, so $\frac{dU_B}{dt} = 0$. The electric energy stored is $U_E = \frac{1}{2}CV^2$. Since $V = Ed$, $U_E = \frac{1}{2}C(Ed)^2 = \frac{1}{2} \frac{\epsilon_0 \pi R^2}{d} (Ed)^2 = \frac{1}{2} \epsilon_0 \pi R^2 d E^2$. Since $E = \frac{It}{\epsilon_0 \pi R^2}$, $E^2 = \frac{I^2 t^2}{(\epsilon_0 \pi R^2)^2}$. So, $U_E = \frac{1}{2} \epsilon_0 \pi R^2 d \frac{I^2 t^2}{(\epsilon_0 \pi R^2)^2} = \frac{1}{2} \frac{I^2 t^2 d}{\epsilon_0 \pi R^2}$. The rate of change of electric energy is $\frac{dU_E}{dt} = \frac{d}{dt} \left(\frac{1}{2} \frac{I^2 t^2 d}{\epsilon_0 \pi R^2}\right) = \frac{1}{2} \frac{I^2 d}{\epsilon_0 \pi R^2} (2t) = \frac{I^2 t d}{\epsilon_0 \pi R^2}$. The magnitude of the Poynting vector at $r=R$ is $S = \frac{EB}{\mu_0}$. At $r=R$, $E = \frac{It}{\epsilon_0 \pi R^2}$ and $B = \frac{\mu_0 I}{2\pi R}$. So, $S = \frac{1}{\mu_0} \left(\frac{It}{\epsilon_0 \pi R^2}\right) \left(\frac{\mu_0 I}{2\pi R}\right) = \frac{I^2 t}{2\pi^2 \epsilon_0 R^3}$. The area of the cylindrical surface at $r=R$ between the plates is $A = 2\pi R d$. The Poynting vector is radially inward, so the flux into the volume is $S \cdot A = \frac{I^2 t}{2\pi^2 \epsilon_0 R^3} (2\pi R d) = \frac{I^2 t d}{\pi \epsilon_0 R^2}$. Let's recheck the electric field calculation. $E = \frac{Q}{\epsilon_0 A} = \frac{It}{\epsilon_0 \pi R^2}$. This is correct. Let's recheck the rate of change of electric energy. $U_E = \frac{1}{2} \epsilon_0 E^2 (\pi R^2 d)$. $\frac{dU_E}{dt} = \frac{1}{2} \epsilon_0 (\pi R^2 d) (2E \frac{dE}{dt}) = \epsilon_0 \pi R^2 d E \frac{dE}{dt}$. $E = \frac{It}{\epsilon_0 \pi R^2}$, so $\frac{dE}{dt} = \frac{I}{\epsilon_0 \pi R^2}$. $\frac{dU_E}{dt} = \epsilon_0 \pi R^2 d \left(\frac{It}{\epsilon_0 \pi R^2}\right) \left(\frac{I}{\epsilon_0 \pi R^2}\right) = \frac{I^2 t d}{\epsilon_0 \pi R^2}$. The flux of the Poynting vector into the volume through the cylindrical surface at $r=R$ is $S \cdot A = \frac{EB}{\mu_0} (2\pi R d)$. $S = \frac{1}{\mu_0} E B = \frac{1}{\mu_0} \left(\frac{It}{\epsilon_0 \pi R^2}\right) \left(\frac{\mu_0 I}{2\pi R}\right) = \frac{I^2 t}{2\pi^2 \epsilon_0 R^3}$. Flux = $S (2\pi R d) = \frac{I^2 t}{2\pi^2 \epsilon_0 R^3} (2\pi R d) = \frac{I^2 t d}{\pi \epsilon_0 R^2}$. Comparing the rate of change of stored energy and the Poynting vector flux into the volume, we see that they are equal. So, option (D) is correct.