Question

A capacitor of capacity ${C_1}$ is charged up to voltage $V$ volt and then connected in parallel to an uncharged capacitor of capacity ${C_2}$ . The final potential difference across each potential difference across each capacitor will be:
A. $\dfrac{{{C_1}V}}{{{C_1} + {C_2}}}$
B. $\dfrac{{{C_2}V}}{{{C_1} + {C_2}}}$
C. $(1 + \dfrac{{{C_1}}}{{{C_2}}})V$
D. $(1 + \dfrac{{{C_2}}}{{{C_1}}})V$

Answer 1

When the two or more capacitors are connected in parallel then the total charge will be the sum of the charge across all capacitors. For example

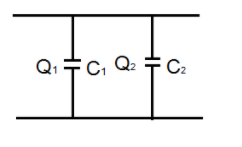
Then total charge $Q$ in the given circuit will be
$Q = {Q_1} + {Q_2}$

Formula used:
$C = \dfrac{Q}{V}$ ……………. (1)
Where $C$ is capacitance, $Q$ is charge, $V$ is voltage
When two capacitor ${C_1}$ and ${C_2}$ are connected in parallel combination then equivalent capacitance ${C_{eq}}$ will be ${C_{eq}} = {C_1} + {C_2}$ ……………. (2)

Complete step by step solution:
Given in question that ${C_1}$ is charged up to $V$
So the charge stored from equation (1) will be ${q_1} = {C_1}V$ …………. (3)
${q_2} = {C_2}V$ …………. (4)
Now capacitors ${C_1}$ and ${C_2}$ are connected in parallel so the potential difference across them will be the same. ${V_A} - {V_B} = \dfrac{{{q_1}}}{{{C_1}}} = \dfrac{{{q_2}}}{{{C_2}}}$ …………… (5)
From equation (5) we can write
${q_1}{C_2} = {q_2}{C_1}$ ……………… (6)
Also from question we know that $q = {q_1} + {q_2}$
And ${q_2} = q - {q_1}$
By putting the value of ${q_2}$ in equation (6)
We get ${q_1}{C_2} = (q - {q_1}){C_1}$
${q_1}{C_2} = q{C_1} - {q_{1}}{C_1}$
${q_1}({C_1} + {C_2}) = {C_1}V.{C_1}$
${q_{1}} = \dfrac{{{C_1}^2V}}{{{C_1} + {C_2}}}$
Hence, $$$$$${V_A} - {V_{B}} = \dfrac{{{q_1}}}{{{C_1}}}$${V_A} - {V_{B}} = \dfrac{{\dfrac{{{C_1}^2V}}{{{C_1} + {C_2}}}}}{{{C_1}}}$${V_A} - {V_B} = \dfrac{{{C_1}V}}{{{C_1} + {C_2}}}$$
So the correct option is (a)

Note:
-In nature we can say an object is in balance if it is not moving, So when an object is moving it is in the state of equilibrium.
The center of gravity is the average position of the force of gravity on a body. Sometimes it is at the object’s geometric center for example ruler, where other times it isn’t (e.g. ruler with an eraser on one end). An object can be balanced or in equilibrium if it is supported directly under its center of gravity.
Common balance can be defined as the balance which is having each arm suspended. The unidentified mass is kept in one arm and the known mass in another until they both become equivalent. Therefore this balance is working on the principle of the moment of weights.