Question

A capacitor of capacitance of $2\mu F$ is connected in the tank circuit of an oscillator oscillating with a frequency of $1kHz$. If current flowing in the circuit is $2mA$, the voltage across the capacitor will be-
(A).$0.16V$
(B).$0.32V$
(C).$79.5V$
(D).$159V$

Answer 1

When a capacitor or inductor is connected in an AC circuit, then reactance is calculated. It is the resistance offered by elements like capacitors and inductors to the flow of current through them. The voltage drop across them is related to the value of their reactance.
Formulas Used:
${{X}_{c}}=\dfrac{1}{\omega C}$
$\omega =2\pi f$
$V=I\times {{X}_{c}}$

Complete answer:

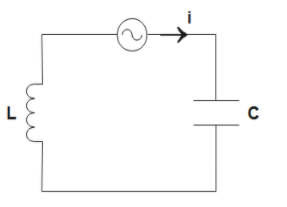
When there are inductors or capacitors connected in a circuit, they tend to oppose the flow of current through them. This property is called reactance ($R$).
For a capacitor, the value of $R$will be-
${{X}_{c}}=\dfrac{1}{\omega C}$ - (1)
Here,
${{X}_{c}}$ is the reactance due to capacitor
$\omega \,$ is the angular velocity
$C$ is the capacitance
We know that,
$\omega =2\pi f$ - (2)
Here, $f$ is the frequency
Substituting eq (2) in eq (1), we get,
${{X}_{c}}=\dfrac{1}{2\pi fC}$

& {{X}_{c}}=\dfrac{1}{2\pi \times {{10}^{3}}\times 2\times {{10}^{-6}}} \\\ & \\\ \end{aligned}$$ $$\Rightarrow {{X}_{c}}=\dfrac{{{10}^{3}}}{4\pi }$$ - (3) The formula for voltage across element of reactance is- $$V=I\times {{X}_{c}}$$ Here,$$V$$ is voltage across the capacitor $$I$$ is the current in the circuit. Substituting values in the above eq, we get, $$\begin{aligned} & V=2\times {{10}^{-3}}\dfrac{{{10}^{3}}}{4\pi } \\\ & \therefore V=0.16V \\\ \end{aligned}$$ The voltage across the capacitor is $$0.16V$$. **Hence, the correct option is (A).** **Additional Information:** AC circuits or alternating current circuits are those circuits in which the value of current and voltage is not constant. The value of current oscillates about a mean value whereas in DC circuits or direct current circuits, the value of current is constant. LC circuits are AC circuits in which a capacitor ($$C$$) and an inductor ($$L$$) are connected together. It is also called a tank circuit **Note:** Capacitors and inductors, both show reactance. When resistors are connected in combination with capacitors or inductors or both, the reactance is called impedance. It is calculated as $$Z=\sqrt{{{X}_{c}}^{2}+{{X}_{i}}^{2}+{{R}^{2}}}$$ . Here, $${{X}_{i}}$$ is reactance of inductors, $$R$$ is resistance.