Question
Question: A capacitor of capacitance \(C\) having initial charge \(2{Q_o}\) is connected to a battery of poten...
A capacitor of capacitance C having initial charge 2Qo is connected to a battery of potential difference V=CQo as shown, then work done by the battery is
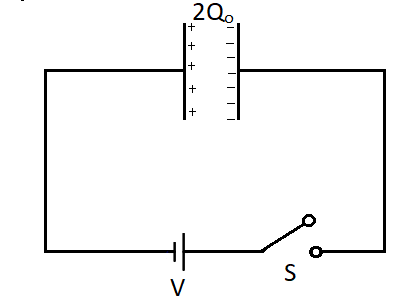
(A) 2CQo2
(B) 2C3Qo2
(C) C3Qo2
(D) 3C2Qo2
Solution
The work done by the battery will be given by the product of the potential across the battery and the charge flow through it. Now, the charge flow in the battery will be the sum of the initial charge across the capacitor and the final charge across it.
In this solution we will be using the following formula,
⇒W=VQ
where W is the work done,
V is the potential and Q is the charge.
Complete step by step solution:
In the question we are given that initially the capacitor is charged to an amount of 2Qo. After that it is connected to a battery. It is given that the potential across the battery is V=CQo. So after the capacitor is connected across the battery, the charge in the capacitor is given by the formula,
⇒Q=CV
On substituting the value we get,
⇒Q=C×CQo
On cancelling the C, we get,
⇒Q=Qo
Therefore, the work done by the battery will be the product of the potential of the battery and the total charge that is flowing from the battery.
Hence,
⇒W=VQ
Substituting we have,
⇒W=CQo×3Qo
On calculating we get,
⇒W=C3Qo2
This is the work done by the battery. So the correct answer is option (C).
Note:
A capacitor is a device that stores electrical energy in a field. The effect in a capacitor is called capacitance. When two electrical conductors are kept in proximity in a circuit, there is some capacitance existing in between them. The capacitor was originally termed as a condenser. In practical use, the capacitors are in the form of metallic plates which are separated by a dielectric medium.
