Question

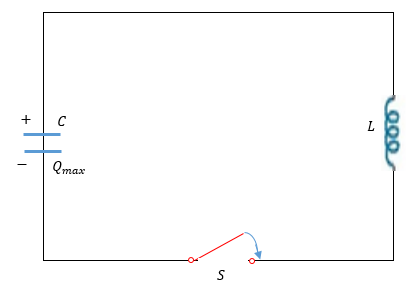
A capacitor of capacitance $C$ has an initial charge ${Q_0}$ and is connected to an inductor of inductance $L$ as shown. At $t = 0$ switch $S$ is closed. The current through the inductor when energy in the capacitor is three times the energy of inductor is

A. $\dfrac{{{Q_0}}}{{2\sqrt {LC} }}$
B. $\dfrac{{{Q_0}}}{{\sqrt {LC} }}$
C. $\dfrac{{2{Q_0}}}{{\sqrt {LC} }}$
D. $\dfrac{{4{Q_0}}}{{\sqrt {LC} }}$

Answer 1

Total energy of a circuit will be the sum of energy of capacitor and energy of inductor.
Formula Used: Energy of Capacitor,${U_c} = \dfrac{{{q^2}}}{{2C}}$
Energy of inductor,${U_I} = \dfrac{1}{2}L{i^2}$

Complete step by step answer:
We know that the energy of capacitor is,${U_c} = \dfrac{{{q^2}}}{{2C}}$
Where,$q$is the charge on the capacitor
$C$is the capacitance of the capacitor.
And energy on inductor is,${U_I} = \dfrac{1}{2}L{i^2}$
Where, $L$is the inductance and, $i$ is the current through the inductor.
It is given that the energy of the capacitor is$3$times the energy of the inductor.
$\Rightarrow {U_c} = 3{U_I}$ . . . (1)
Now,
since, the initial change of the circuit is${Q_0}$.
Total energy${U_T} = \dfrac{{{Q_0}^2}}{{2C}}$ . . . (2)
We also know that the total energy
${U_T} = {U_c} + {U_I}$
$\Rightarrow {U_T} = 3{U_I} + {U_I}$ from equation (1)
$\Rightarrow {U_T} = 4{U_I}$.
Now substitute the valence of${U_T}$and${U_I}$ in the above equation.
$\Rightarrow \dfrac{{{Q_0}^2}}{{2C}} = 4 \times \dfrac{1}{2}L{i^2}$
$\Rightarrow \dfrac{{{Q_0}^2}}{C} = 4L{i^2}$
By rearranging it, we get
${i^2} = \dfrac{{{Q_0}^2}}{{4LC}}$
Taking square root to both the sides, we get
${i^2} = \dfrac{{{Q_0}}}{{2\sqrt {LC} }}$
Therefore, from the above explanation the correct option is A. $\dfrac{{{Q_0}}}{{2\sqrt {LC} }}$.

Note: Capacitor is a device that stones electrical energy in electric fields.
Inductor is a device that stores energy in a magnetic field when electric current is passed through it.
Since, inductor does not have a sparkle initial change on it, the initial charge on the capacitor was the total charge of the circuit. That is why we could write,${U_T} = \dfrac{{{Q_0}^2}}{{2C}}$.