Question

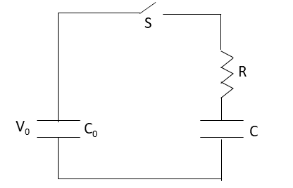
A capacitor of capacitance ${C_0}$ is charged to a potential ${V_0}$ and is connected with another capacitor of capacitance $C$ as shown. After closing the switch S, the common potential across the two capacitors becomes $V$. The capacitance $C$ is given by

A. $\dfrac{{{C_0}\left( {{V_0} - V} \right)}}{{{V_0}}}$
B. $\dfrac{{{C_0}\left( {V - {V_0}} \right)}}{{{V_0}}}$
C. $\dfrac{{{C_0}\left( {V + {V_0}} \right)}}{V}$
D. $\dfrac{{{C_0}\left( {{V_0} - V} \right)}}{V}$

Answer 1

Use the formula for charge on the plates of the capacitor. This formula gives the relation between the charge on the plates of the capacitor, capacitance of the capacitor and potential difference between the plates of the capacitor. Determine the charge on all the capacitors before and after closing the switch S. Use the law of conservation of charge and derive the expression for the capacitor C.

Formula used:
The charge $Q$ stored on the plates of the capacitor is given by
$Q = CV$ …… (1)
Here, $C$ is capacitance of the capacitor and $V$ is the potential difference between the plates of the capacitor.

Complete step by step answer:
We have given that the capacitance of the capacitor ${C_0}$ has potential difference of ${V_0}$.
According to equation (1), the initial charge ${Q_i}$ stored on the plates of the capacitor of capacitance ${C_0}$ is
${Q_i} = {C_0}{V_0}$
When the switch S is closed, the common potential difference across the two capacitors of capacitances ${C_0}$ and $C$ is $V$.
We have asked to calculate the capacitance $C$ when the switch S is closed.Hence, the charge ${Q_{f1}}$ stored on the capacitor ${C_0}$ when the switch S is closed is
${Q_{f1}} = {C_0}V$
Hence, the charge ${Q_{f2}}$ stored on the capacitor $C$ when the switch S is closed is
${Q_{f2}} = CV$

According to the law of conservation of charge, the initial charge on the capacitor ${C_0}$ is equal to the total charge on the capacitors ${C_0}$ and $C$ when the switch S is closed.
${Q_i} = {Q_{f1}} + {Q_{f2}}$
Substitute ${C_0}{V_0}$ for ${Q_i}$, ${C_0}V$ for ${Q_{f1}}$ and $CV$ for ${Q_{f2}}$ in the above equation.
${C_0}{V_0} = {C_0}V + CV$
$\Rightarrow CV = {C_0}{V_0} - {C_0}V$
$\therefore C = \dfrac{{{C_0}\left( {{V_0} - V} \right)}}{V}$
Therefore, the value of the capacitance C is $\dfrac{{{C_0}\left( {{V_0} - V} \right)}}{V}$.

Hence, the correct option is D.

Note: The students may not get confused that the potential difference between the two capacitors is different. But the students should keep in mind that the potential difference between the two capacitors is the same as these two capacitors are connected in parallel. Hence, we have used the same value of potential difference when the switch S is closed.