Solveeit Logo
Login

Question

Question: A capacitor of capacitance \(6\mu F\) is charged to a potential of 150V. Its potential falls to 90V,...

A capacitor of capacitance 6μF6\mu F is charged to a potential of 150V. Its potential falls to 90V, when another capacitor is connected to it. Find the capacitance of the second capacitor and the amount of energy lost due to connection.

Explanation

Solution

When capacitors were connected in series charge remains the same on capacitors but in parallel voltage remains same across the capacitors and by the conservation of charge we can proceed to solve the above problem.

Formula used:
To solve this problem we will be using conservation of charge which is given by,C1V1=(C1+C2)V2{{C}_{1}}{{V}_{1}}=\left( {{C}_{1}}+{{C}_{2}} \right){{V}_{2}}
To calculate energy stored in the capacitor
12CV2\dfrac{1}{2}C{{V}^{2}} will be used here.

Complete Step by step solution:
First,6μF6\mu F capacitor charged to potential of 150V now when another capacitor is connected potential drops to 90V So,

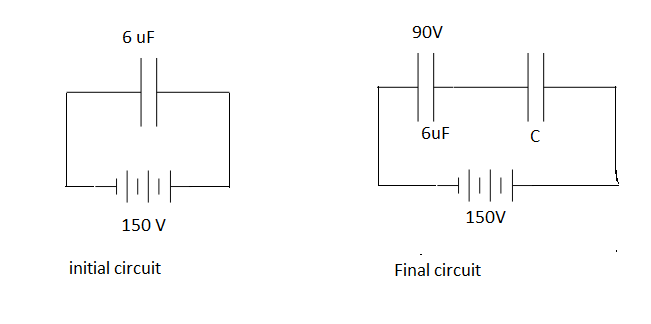
C1=6μF{{C}_{1}}=6\mu F
V1=150V{{V}_{1}}=150V

Final C=C1+C2{{C}_{1}}+{{C}_{2}} and,
V2=90V{{V}_{2}}=90V

We know that charge will remain conserved so,
C1V1=(C1+C2)V2{{C}_{1}}{{V}_{1}}=\left( {{C}_{1}}+{{C}_{2}} \right){{V}_{2}}
6μF×150=(6μF+C2)×906\mu F\times 150=(6\mu F+{{C}_{2}})\times 90
6μF+C2=6μF×15090=10μF6\mu F+{{C}_{2}}=\dfrac{6\mu F\times 150}{90}=10\mu F=CF{{C}_{F}}
C2=4μF{{C}_{2}}=4\mu F

Now, Energy for calculating energy loss we need to subtract final energy with initial energy,
Energy can be defined as 12CV2\dfrac{1}{2}C{{V}^{2}}so,
Energy loss=EF−EI{{E}_{F}}-{{E}_{I}}
12CFV2−12CiV2\dfrac{1}{2}{{C}_{F}}{{V}^{2}}-\dfrac{1}{2}{{C}_{i}}{{V}^{2}}
=12(10×(90)2)−(6×(150)2)=\dfrac{1}{2}\left( 10\times {{(90)}^{2}} \right)-\left( 6\times {{(150)}^{2}} \right)
Energy Loss=27×10−3J=27\times {{10}^{-3}}J

So, after inserting new capacitor into the circuit the energy loss due to connection will be equal to =27×10−3J=27\times {{10}^{-3}}J

Additional information:
In these types of problems we need to carefully observe the connections and how the additional capacitor can be added into the circuit (series or parallel) according to the voltage data given in the question. To calculate energy loss due to connections try to calculate initial and final energies with the given data and solve accordingly to calculate total energy loss.

Note:
To calculate capacitance of new capacitor we need to conserve total charge in the system and for loss in energy we need to subtract final final energy to initial energy which cause due to addition of new capacitor by which due to some external factors and resistance energy releases in different forms.