Question
Question: A capacitor of capacitance 2C is charged with charge $q_0$ is connected in series with an uncharged ...
A capacitor of capacitance 2C is charged with charge q0 is connected in series with an uncharged capacitor and inductor of inductance L. Find maximum value of current through the inductor.
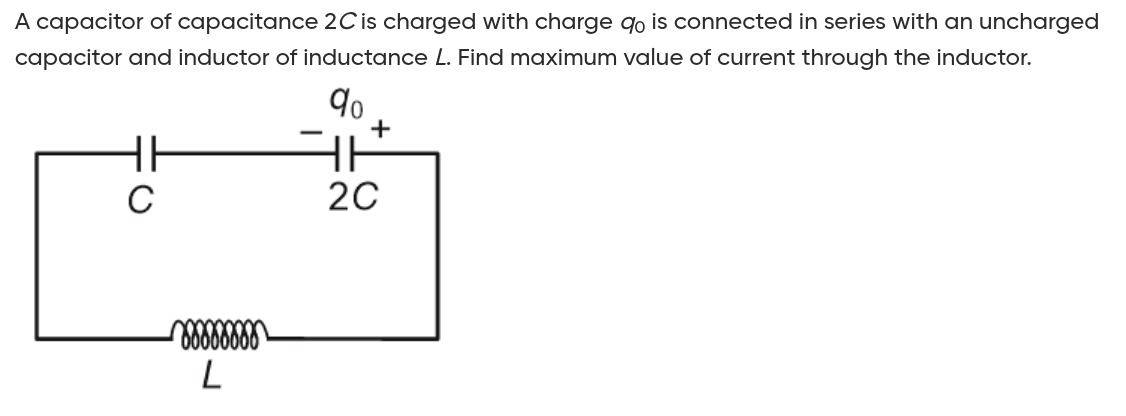
3LCq0
6LCq0
2LCq0
LCq0
6LCq0
Solution
The initial energy stored in the charged capacitor (C1=2C) is Einitial=2(2C)q02=4Cq02.
When the capacitors (C1=2C and C2=C) are in series, the equivalent capacitance is Ceq=C1+C2C1C2=2C+C(2C)(C)=3C2C2=32C.
The maximum current in an LC circuit occurs when all the initial energy is converted into magnetic energy in the inductor, i.e., when the charge on the capacitors is zero. However, in this case, the capacitors are in series, and the charge distribution changes.
The total energy is conserved: Einitial=4Cq02. At maximum current, the energy is purely magnetic: Emax_current=21LImax2. This occurs when the charge distribution across the capacitors is such that the total energy stored in the capacitors is minimized, and the remaining energy is in the inductor.
Alternatively, consider the total energy in the system. When the current is maximum, the energy stored in the capacitors is minimal. The charge on C1 is q1 and on C2 is q2. Since they are in series, q1=q2=qseries. The total energy is E=2C1q12+2C2q22+21LI2=2(2C)qseries2+2Cqseries2+21LI2=4C3qseries2+21LI2. The initial energy is 4Cq02. This initial charge q0 is on C1. When connected, charge redistributes. The total charge on the series combination is qseries. The initial energy is 4Cq02. The maximum current occurs when the total energy is 21LImax2. By conservation of energy, 4Cq02=21LImax2. This assumes the final charge on both capacitors is zero, which is not always true.
A more rigorous approach: The total initial energy is Ui=4Cq02. At maximum current, the energy is Umax_I=21LImax2. This energy comes from the initial potential energy. The total charge on the series combination is Q. The voltage across C1 is V1=Q/(2C) and across C2 is V2=Q/C. The initial charge q0 is on 2C. So the initial voltage is V0=q0/(2C). When connected, V1=V2 if no inductor is present. With an inductor, the total energy is conserved. E=4Cq12+2Cq22+21LI2. Initially, q1=q0, q2=0, I=0. E=4Cq02. At maximum current, I=Imax, and the charge on capacitors is such that the total potential energy is minimal. The charge on C1 is q0−q and on C2 is q. Ucap=4C(q0−q)2+2Cq2. dUcap/dq=−2Cq0−q+Cq=2C−q0+q+2q=2C3q−q0. Setting dUcap/dq=0, we get q=q0/3. Then q1=q0−q0/3=2q0/3 and q2=q0/3. The minimum capacitor energy is Ucap,min=4C(2q0/3)2+2C(q0/3)2=4C4q02/9+2Cq02/9=9Cq02+18Cq02=18C3q02=6Cq02. By conservation of energy: Einitial=Ucap,min+21LImax2. 4Cq02=6Cq02+21LImax2. 21LImax2=4Cq02−6Cq02=12C3q02−2q02=12Cq02. Imax2=6LCq02. Imax=6LCq0.
