Question

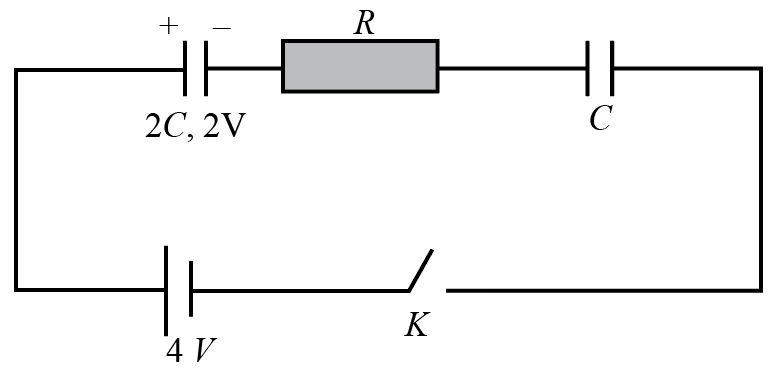
A capacitor of capacitance 2C is charged to a potential 2V and then connected to an uncharged capacitor of capacitance C with a resistance R to a battery of emf 4V as shown.
The key is closed at $t = 0$. The charge on the uncharged capacitor as a function of time will be

Answer 1

We will use the concept of charge of a capacitor which is given by the product of its capacitance and voltage. From the concept of Kirchhoff’s law, we know that the summation of total voltage in an electric circuit is equal to the voltage supplied to the circuit with external power supplies.

Complete step by step answer:
Let us write the expression for the charge on the capacitor of capacitance 2C.
${q_0} = {C_0}{V_0}$
Here ${C_0}$ is the capacitance and ${V_0}$ is the potential difference across the capacitor.

We will substitute 2C for ${C_0}$ and 2V for ${V_0}$ in the above expression.
${q_0} = \left( {2{\rm{ C}}} \right)\left( {2{\rm{ V}}} \right)\\\ = 4{\rm{ F}}$

We know that 2C capacitor will discharge as time progresses so at after time t we can write the expression for the charge on a capacitor of capacitance 2C as below:
$q' = {q_0} - q$
Here q is the amount of charge discharged and q’ is the amount of charge on the capacitor at time t.

The charge q which is discharged from 2C capacitor is used to charge the capacitor of capacitance C so we can write that the charge on a capacitor of capacitance C as below:
${q_2} = q$

Using the concept of Kirchhoff’s law for the given circuit, we can write:
$IR + \dfrac{{{q_2}}}{C} + \dfrac{{q'}}{{2C}} = 4V$

We will substitute q for ${q_2}$ and ${q_0} - q$ for q’ in the above expression.
$IR + \dfrac{q}{C} + \dfrac{{{q_0} - q}}{{2C}} = 4{\rm{ V}}\\\ \implies IR = 4{\rm{ V}} - q\left( {\dfrac{1}{C} - \dfrac{1}{{2C}}} \right) - \dfrac{{{q_0}}}{{2C}}\\\ \implies IR = 4{\rm{ V}} - q\left( {\dfrac{1}{C} - \dfrac{1}{{2C}}} \right) - \dfrac{{{q_0}}}{{2C}}\\\ \implies IR = 4{\rm{ V}} - \dfrac{q}{{2C}} - \dfrac{{{q_0}}}{{2C}}$……(1)

We know that current is equal to the change of charge with respect to time so we can write:
$I = \dfrac{{dq}}{{dt}}$

We will substitute $\dfrac{{dq}}{{dt}}$ for I in equation (1).
$\dfrac{{dq}}{{dt}}R = 4{\rm{ V}} - \dfrac{q}{{2C}} - \dfrac{{{q_0}}}{{2C}}\\\$
Writing the above equation in the form of a differential equation, we get:
$\dfrac{{dq}}{{dt}} + \dfrac{q}{{2R}} = \dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}$

We can write the expression for integrating factors of the above differential equation.
$I.F. = {e^{\int\limits_0^t {\dfrac{1}{{2R}}dt} }}\\\ \implies I.F. = {e^{\dfrac{1}{{2R}}\left[ t \right]_0^t}}\\\ \implies I.F. = {e^{\dfrac{t}{{2R}}}}$

Using the final expression for the solution of the given differential equation, we can write:
$q \cdot I.F. = \int {\left( {\dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}} \right)} \cdot I.F.dt$

We will substitute ${e^{\dfrac{t}{{2R}}}}$ for I.F. in the above expression.
$q \cdot {e^{\dfrac{t}{{2R}}}} = \int {\left( {\dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}} \right)} \cdot {e^{\dfrac{t}{{2R}}}}dt\\\ = \left( {\dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}} \right)\dfrac{{{e^{\dfrac{t}{{2R}}}}}}{{2R}} + C$……(2)
We know at the time $t = 0$, the value of charge q is zero so we can substitute 0 for q in the above expression to get the value of constant C.
$0 \cdot {e^{\dfrac{0}{{2R}}}} = \left( {\dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}} \right)\dfrac{{{e^{\dfrac{0}{{2R}}}}}}{{2R}} + C\\\ \implies C = \dfrac{{{q_0} - 8}}{{4{R^2}}}$

We will substitute $\left( {\dfrac{{{q_0} - 8}}{{4{R^2}}}} \right)$ for C in equation (2) to get the final expression.
$q \cdot {e^{\dfrac{t}{{2R}}}} = \left( {\dfrac{4}{R} - \dfrac{{{q_0}}}{{2R}}} \right)\dfrac{{{e^{\dfrac{t}{{2R}}}}}}{{2R}} + \dfrac{{{q_0} - 8}}{{4{R^2}}}$.

Note:
For the differential equation given in the form $\dfrac{{dx}}{{dy}} + Px = Q$, its general solution is obtained by integrating factor methods. The value of integrating factor is $I.F. = {e^{\int {Pdy} }}$ , and the expression for the general solution is expressed as:
$x\left( {I.F.} \right) = \int Q \left( {I.F.} \right)dy$