Question

A capacitor of capacitance $100\mu F$ is connected to a battery of 20 volts for a long time and then disconnected from it. It is now connected across a long solenoid having 4000turns per meter. It is found that the potential difference across the capacitor drops to 90% of its maximum value in 2.0 seconds. Estimate the average magnetic field produced at the centre of the solenoid during this period.

Answer 1

Initially the capacitor is connected to a d.c. supply for an appreciable amount of time. Hence the capacitor will get fully charged such that the potential difference across the capacitor will be equal to that of the battery. Further when connected to any other circuit component it will get discharged i.e. the charge on the capacitor will gradually decrease. The difference in the charge with time across the capacitor will give us the current in the circuit with which we can determine the average magnetic field produced across the solenoid.
Formula used:
$B={{\mu }_{\circ }}ni$
$q=CV$
$i=\dfrac{\Delta q}{t}$

Complete answer:

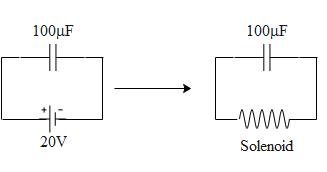
From the above diagram we see the two cases one when the capacitor is connected ted the battery and one when it is connected to the solenoid. Let us say we connect a capacitor of capacitance ‘C’ to battery of emf ‘V’. then the charge ‘q’ developed across the capacitor is given by,
$q=CV$
Since capacitor of capacitance $100\mu F$ is connected a battery of 20 volts for a long time, the charge on the capacitor is equal to,
$\begin{aligned} & q=CV \\\ & \Rightarrow q=100\mu F\times 20V \\\ & \therefore q=2\times {{10}^{-3}}C \\\ \end{aligned}$
Further when the capacitor is connected to the solenoid it is given that the potential ‘E’ drop across the capacitor is 90% of its initial value i.e.
$\begin{aligned} & E=90\%(20) \\\ & \Rightarrow E=0.9(20)V \\\ & \therefore E=18V \\\ \end{aligned}$
Therefore when the potential reduces to 18V across the capacitor, the charge on the capacitor would be,
$\begin{aligned} & Q=CE \\\ & \Rightarrow Q=100\mu F\times 18V \\\ & \therefore Q=1.8\times {{10}^{-3}}C \\\ \end{aligned}$
This charge lost by the capacitor i.e. $\Delta q=(q-Q)$ actually drives the current in the circuit. It is given to us that the capacitor loses this charge in t=2.0 seconds. Since current in the circuit is defined as the rate of flow of charge, the current at that instant of time is equal to,
$\begin{aligned} & i=\dfrac{\Delta q}{t} \\\ & \Rightarrow i=\dfrac{q-Q}{t} \\\ & \Rightarrow i=\dfrac{2\times {{10}^{-3}}C-1.8\times {{10}^{-3}}C}{2s} \\\ & \Rightarrow i=\dfrac{0.2\times {{10}^{-3}}C}{2s} \\\ & \therefore i=0.1\times {{10}^{-3}}A \\\ \end{aligned}$
The magnetic field at the center of the solenoid with ‘n’ number of turns per unit length is given by,
$\begin{aligned} & B={{\mu }_{\circ }}ni \\\ & \because n=4000,\text{ }i=0.1\times {{10}^{-3}}A \\\ & \Rightarrow B=4\pi \times {{10}^{-7}}\times 4000\times 0.1\times {{10}^{-3}}A \\\ & \therefore B=16\pi \times {{10}^{-8}}T \\\ \end{aligned}$
Therefore the average magnetic field at the produced at the centre of the solenoid during period of 2 seconds is $16\pi \times {{10}^{-8}}T$

Note:
The magnetic field produced at the center is the average magnetic field as the field along the length varies.${{\mu }_{\circ }}$ is called as the permeability of free space having a value of $4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$ . It is to be noted that we have considered an ideal solenoid which has half the value of the magnetic field at its ends as that of its center.