Question
Question: A capacitor of \[4\,\mu {\text{F}}\] is connected in the circuit. The internal resistance of the bat...
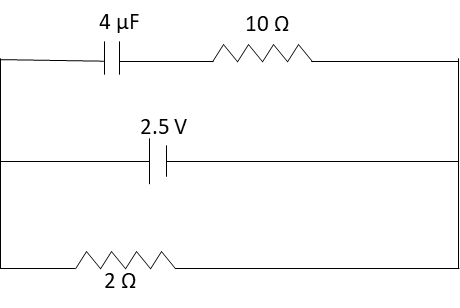
A capacitor of 4μF is connected in the circuit. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
A. 0
B.4μC
C.16μC
D.8μC
Solution
Use the equation for the electric current flowing through the main resistance and the internal resistance. Also, use the expression for Ohm’s law and determine the potential difference across the internal resistance and then capacitor. Use the equation for the charge stored on the plates of the capacitor.
Formula used:
The current I flowing through the main resistance and the internal resistance is
I=R+rV …… (1)
Here, V is the potential difference, R is the main resistance and r is the internal resistance.
The expression for Ohm’s law is
V=IR …… (2)
Here, V is the potential difference, I is the current and R is the resistance.
The charge stored Q on the capacitor is
Q=CV …… (3)
Here, C is the capacitance and V is the potential difference across the plates of the capacitor.
Complete step by step answer:
From the given circuit diagram, it can be seen that no current flows through the resistor with resistance 10Ω as the capacitor is open circuited.
We have given that the internal resistance of the battery is 0.5Ω.
r=0.5Ω
We can determine the current flowing through the main and internal resistance using equation (1).
Substitute 2.5V for V, 2Ω for R and 0.5Ω for r in equation (1).
I=(2Ω)+(0.5Ω)2.5V
⇒I=1A
Hence, the current flowing through the lower arm of the given circuit is 1A.
We can calculate the potential difference Vr across the internal resistance.
Substitute 1A for I and 0.5Ω for r in equation (2).
Vr=(1A)(0.5Ω)
⇒Vr=0.5V
Hence, the potential difference across the internal resistance is 0.5V.
The potential difference Vc across the 4μF capacitor is the difference of the potential difference V of the battery and the potential difference Vr across the internal resistance.
Vc=V−Vr
Substitute 2.5V for V and 0.5V for Vr in the above equation.
Vc=2.5V−0.5V
⇒Vc=2V
This gives the potential difference across the capacitor.
Let us now calculate the amount of charge through the capacitor.
Substitute 4μF for C and 2V for V in equation (3).
Q=(4μF)(2V)
⇒Q=(4×10−6F)(2V)
⇒Q=8μC
Therefore, the amount of charge on the capacitor plates is 8μC.
Hence, the correct option is D.
Note:
The students may determine the current flowing through the circuit considering all the resistors connected in the circuit. But the capacitor is open circuited and hence, no current flows through the 10Ω resistor. So, this resistor should not be considered while determining the current through the circuit.
