Solveeit Logo
Login

Question

Question: A capacitor of \[2\mu F\] is charged as shown in the diagram. When the switch \[S\] is turned to pos...

A capacitor of 2μF2\mu F is charged as shown in the diagram. When the switch SS is turned to position 22 , the percentage of its stored energy dissipated is:

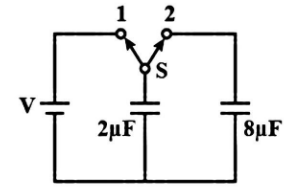
A. 0%0\%
B. 20%20\%
C. 75%75\%
D. 80%80\%

Explanation

Solution

In order to solve this question first of all we will find the initial energy of capacitance and then find the final energy stored in the capacitor formula of energy stored in a capacitor. After that inorder to get the heat dissipated in the circuit we will find the difference between the final and initial energy.

Complete step by step answer:
Initially, the energy stored in 2μF2\mu F capacitor is
Ui=12CV2 ⇒Ui=12(2×10−6)V2 ⇒Ui=V2×10−6J{U_i} = \dfrac{1}{2}C{V^2} \\\ \Rightarrow {U_i} = \dfrac{1}{2}\left( {2 \times {{10}^{ - 6}}} \right){V^2} \\\ \Rightarrow {U_i} = {V^2} \times {10^{ - 6}}J
Initially, the charge stored in 2μF2\mu F capacitor is Qi=CV=(2×10−6)V=2V×10−6{Q_i} = CV = \left( {2 \times {{10}^{ - 6}}} \right)V = 2V \times {10^{ - 6}} Coulomb. When switch SS Is turned to position 2, the charge flow and both the capacitors share charges till a common potential VC{V_C} is reached.
VC=total chargetotal capacitance ⇒VC=2V×10−6(2+8)×10−6⇒VC=V5volt {V_C} = \dfrac{{total\,charge}}{{total\,capacitance}} \\\ \Rightarrow {V_C} = \dfrac{{2V \times {{10}^{ - 6}}}}{{\left( {2 + 8} \right) \times {{10}^{ - 6}}}} \Rightarrow {V_C} = \dfrac{V}{5}volt \\\
Therefore, finally the energy stored in both the capacitors is
Uf=12[(2+8)×10−6](V5)2 ⇒Uf=V25×10−6J {U_f} = \dfrac{1}{2}\left[ {\left( {2 + 8} \right) \times {{10}^{ - 6}}} \right]{\left( {\dfrac{V}{5}} \right)^2} \\\ \Rightarrow {U_f}= \dfrac{{{V^2}}}{5} \times {10^{ - 6}}J \\\
%\% Loss of energy, ΔU=Ui−UfUi×100%\Delta U = \dfrac{{{U_i} - {U_f}}}{{{U_i}}} \times 100\%
ΔU=(V2−V25)×10−6V2×10−6×100% ∴ΔU=80%\Delta U = \dfrac{{\left( {\dfrac{{{V^2} - {V^2}}}{5}} \right) \times {{10}^{ - 6}}}}{{{V^2} \times {{10}^{ - 6}}}} \times 100\% \\\ \therefore \Delta U= 80\%

Hence the correct option is D.

Note: One should take care that there is no flow of charge in open circuit, in order to maintain the flow of change closed circuit is must. When the switch is shifted from one position to another then there will be a change in the charge flowing path which will change the energy and hence there will be some heat loss.