Question
Question: A capacitor is half-filled with a dielectric \(\left( {\kappa = 2} \right)\) as shown in figure A. I...
A capacitor is half-filled with a dielectric (κ=2) as shown in figure A. If the same capacitor is to be filled with the same dielectric as shown, what would be the thickness of the dielectric so the capacitor has the same capacity?
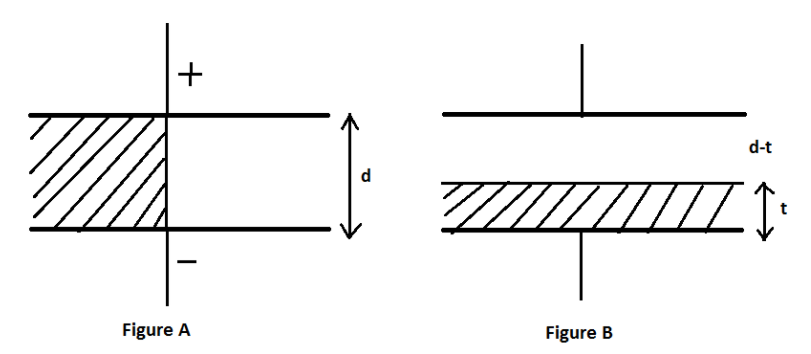
A. 32d
B. 23d
C. 43d
D. 34d
Solution
We have to analyze the figure carefully. As the parallel plate capacitor is half-filled with dielectric, the other half is filled with air which also acts as a dielectric with dielectric constant 1 (κ=2). So we have to consider two dielectrics in both the figures and find out if they are in parallel combination of series combination and according to that use the formula of capacitance.
Complete step by step answer:
We know the formula of the capacitance of a parallel plate capacitor to be,
When air is in between the plates, the capacitance is given by:
C=dεoA
Where,
C is the capacitance.
εo is the permittivity of free space.
A is the area of the plates.
d is the distance between the plates.
When a dielectric is inserted between the plates with dielectric constant,κ the capacitance is given b
C=dεoκA......(1)
Where,
C is the capacitance.
εo is the permittivity of free space.
A is the area of the plates.
d is the distance between the plates.
κ is the dielectric constant.
Now, from our knowledge of parallel and series combination of dielectrics we know that:
For the dielectric in series, the capacitance will be,
C1eq=C11+C21
Where,
Ceq is the equivalent capacitance.
C1&C2 are the capacitance of the two individual capacitors in combination.
For the dielectric in series, the capacitance will be,
Ceq=C1+C2
Where,
Ceq is the equivalent capacitance.
C1&C2 are the capacitance of the two individual capacitors in combination.
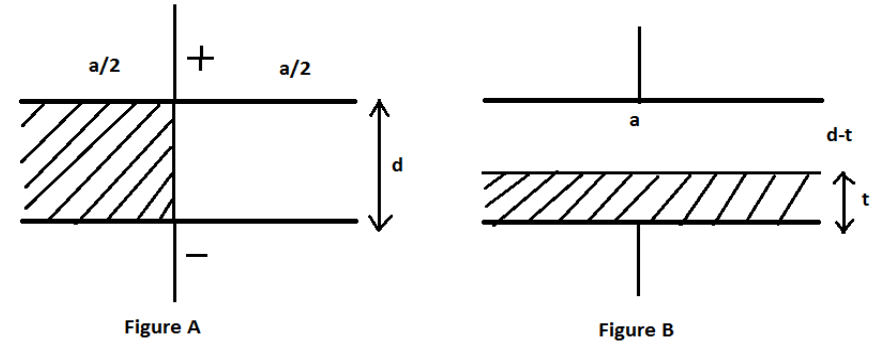
Now, in figure A, we have the distance between the plates as ‘ d ‘which is equal to the thickness of dielectric in the half portion. Let the area of the plates of the capacitor in figure A be ‘ a ‘. It is given that the area covered by the dielectric and the area covered by air between the plates is 2a . We will use the formula in equation (1) to find the individual capacitance. Therefore, the capacitance of the capacitor with dielectric κ=2 is given by,
C1=2dεoκa......(2)
Similarly, the capacitance of the capacitor with air as a dielectric κ=1 is given by,
C2=2dεoa.....(3)
In figure A, the dielectrics are in parallel combination. So, we use:
Ceq=C1+C2......(4)
Where, Ceq is the equivalent capacitance, C1 is the capacitance of the capacitor with dielectric κ=2 in combination and C2 is the capacitance of the capacitor with air as a dielectric κ=1 in combination.
We have to put equations (2) & (3) in equation (4) we get,
Ceq=C1+C2
⇒Ceq=2dεoκa+2dεoa
⇒Ceq=2dεoa(κ+1)
But, for the dielectric κ=2, therefore,
Ceq=2dεoa(2+1)
⇒Ceq=2d3εoa......(5)
Here in figure B, we have to notice that now the thickness of the dielectric is ‘t ‘. So, the remaining portion having air as a dielectric is (d−t). Here the area of the plates of the capacitor will be ‘a‘ as the dielectric is filled horizontally. The new capacitance of the capacitor with dielectric κ=2would be: the capacitor with dielectric κ=2
C1′=tεoκa.......(6)
Similarly, the capacitance of the capacitor with air as a dielectric κ=1 is given by,
C2′=d−tεoa......(7)
We now consider figure B where the dielectrics are in series combination. Therefore, the equivalent capacitance would be,
Ceq′1=C1′1+C2′1.....(8)
We have to put the values of equation (6) and (7) in equation (8) we get,
⇒Ceq′1=(tεoκa)1+(d−tεoa)1
⇒Ceq′1=εoκat+εoad−t
By solving the above equation we get,
Ceq′1==εoκat+εoad−t
⇒Ceq′1=εoκaκ(d−t)+t
⇒Ceq′1=εoκa2(d−t)+t
⇒Ceq′1=εoκa2d−2t+t
⇒Ceq′1=εoκa2d−t
Therefore, the equivalent capacitance is given by:
Ceq′=2d−tεoκa
⇒Ceq′=2d−t2εoa.......(9)
According to the question, we have to equate equation (5) and equation (9) as they both have the same capacitance. We get,
Ceq=Ceq′
⇒2d3εoa=2d−t2εoa
⇒3(2d−t)=2×2d
⇒6d−3t=4d
∴t=32d
So, option (A) is the correct answer.
Note: If the capacitors are in parallel combination, it implies that the voltage across each one is the same. So if we replace it with an equivalent capacitor then the equivalent charge would be the sum of all the charges in the capacitor. Now, when the capacitor is connected in series, the magnitude of the charge on the capacitor would be the same and the total potential difference is the sum of the potential difference across each one.Dielectric is a non-conducting material which when placed between the plates of the capacitor, its molecules gets polarized.
