Question

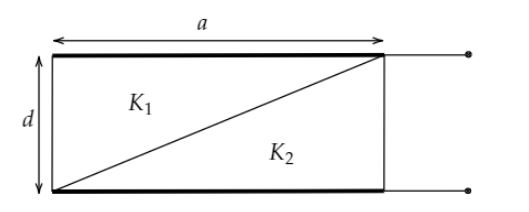
A capacitor is formed by two square metal-plates of edge separated by a distance $d$. Dielectrics of dielectric constants $K_1$ and $K _ 2$ are filled in the gap as shown in the figure. Find the capacitance.

Answer 1

The given capacitor can be considered as two capacitors connected in series. Take an elementary section of the given capacitor and then apply the formula of capacitance $C = \dfrac{{K{\varepsilon _0}A}}{d}$ to find the elementary capacitances of upper part and lower part. Apply the formula $\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$ for series connection. Integrate the elementary capacitance over the whole region to get total capacitance of the given capacitor.

Complete step by step answer:
It is given that the edge of the two square metal-plates is $a$. The distance between the metal-plates is $d$. The given capacitor is filled with dielectrics of dielectric constant ${K_1}$ and ${K_2}$. We can consider the given capacitor as two capacitors ${C_1}$ and ${C_2}$ connected in series. ${C_1}$ and ${C_2}$filled with dielectric constants ${K_1}$ and ${K_2}$ respectively. Let’s draw a diagram to understand easily.

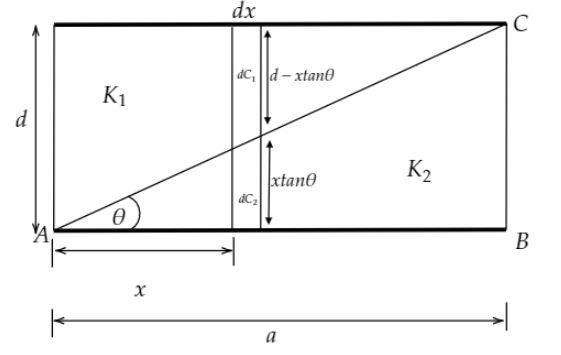
Consider an elementary section of the given capacitor as shown in the above diagram. The upper part is $d{C_1}$ filled with ${K_1}$ and the lower part is $d{C_2}$ filled with ${K_2}$.$\theta$ be the angle of the lower right-angled triangle ABC as shown in the above figure.Then, the length of the lower elementary capacitor $d{C_2}$ will be $x\tan \theta$.The length of the upper elementary capacitor $d{C_1}$ will be $d - x\tan \theta$. We know that the formula of capacitance of a parallel plates capacitor is,
$C = \dfrac{{K{\varepsilon _0}A}}{d}$.
Now, $d{C_1} = \dfrac{{{K_1}{\varepsilon _0}\left( {adx} \right)}}{{d - x\tan \theta }}$
And, $d{C_2} = \dfrac{{{K_2}{\varepsilon _0}\left( {adx} \right)}}{{x\tan \theta }}$

Both the elementary capacitors of capacitance $d{C_1}$ and $d{C_2}$ connected in series.The effective capacitance $dC$ is given by
$\dfrac{1}{{dC}} = \dfrac{1}{{d{C_1}}} + \dfrac{1}{{d{C_2}}}$
Substitute the required values in the above formula.
$\Rightarrow \dfrac{1}{{dC}} = \dfrac{{d - x\tan \theta }}{{{K_1}{\varepsilon _0}adx}} + \dfrac{{x\tan \theta }}{{{K_2}{\varepsilon _0}adx}}$
Simplify the above equation
$\Rightarrow \dfrac{1}{{dC}} = \dfrac{{{K_2}\left( {d - x\tan \theta } \right) + {K_1}\left( {x\tan \theta } \right)}}{{{K_1}{K_2}a{\varepsilon _0}dx}}$
$\Rightarrow \dfrac{1}{{dC}} = \dfrac{{{K_2}d + \left( {{K_1} - {K_2}} \right)x\tan \theta }}{{{K_1}{K_2}a{\varepsilon _0}dx}}$
$\Rightarrow dC = \dfrac{{{K_1}{K_2}a{\varepsilon _0}dx}}{{{K_2}d + \left( {{K_1} - {K_2}} \right)x\tan \theta }}$

Now integrate the above equation over the whole region to obtain the total capacitance.
$\int_0^C {dC} = \int_0^a {\dfrac{{{K_1}{K_2}a{\varepsilon _0}}}{{{K_2}d + \left( {{K_1} - {K_2}} \right)x\tan \theta }}dx}$
$\Rightarrow C = {K_1}{K_2}a{\varepsilon _0}\int_0^a {\dfrac{1}{{{K_2}d + \left( {{K_1} - {K_2}} \right)x\tan \theta }}dx}$
We know the formula of integration $\int {\dfrac{{dx}}{{Ax + B}} = \dfrac{1}{A}\ln \left| {Ax + B} \right|} + C$. We got,
$\Rightarrow C = \dfrac{{{K_1}{K_2}a{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)\tan \theta }}\left[ {\ln \left| {{K_2}d + \left( {{K_1} - {K_2}} \right)x\tan \theta } \right|} \right]_0^a$
Further simplify. We got,
$\Rightarrow C = \dfrac{{{K_1}{K_2}a{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)\tan \theta }}\left[ {\ln \left| {{K_2}d + \left( {{K_1} - {K_2}} \right)a\tan \theta } \right| - \ln \left| {{K_2}d} \right|} \right]$

From the above figure, in the right-angled triangle ABC, $\tan \theta = \dfrac{d}{a}$
$\Rightarrow C = \dfrac{{{K_1}{K_2}{a^2}{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)}}\left[ {\ln \left| {{K_2}d + \left( {{K_1} - {K_2}} \right)d} \right| - \ln \left| {{K_2}d} \right|} \right]$
$\Rightarrow C = \dfrac{{{K_1}{K_2}{a^2}{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)}}\left[ {\ln \left| {{K_1}d} \right| - \ln \left| {{K_2}d} \right|} \right]$
Also, we know the logarithmic formula $\ln A - \ln B = \ln \left( {\dfrac{A}{B}} \right)$
$\Rightarrow C = \dfrac{{{K_1}{K_2}{a^2}{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)}}\left( {\ln \left| {\dfrac{{{K_1}d}}{{{K_2}d}}} \right|} \right)$
$\therefore C = \dfrac{{{K_1}{K_2}{a^2}{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)}}\left( {\ln \left| {\dfrac{{{K_1}}}{{{K_2}}}} \right|} \right)$

Hence, the capacitance of the given capacitor is $\dfrac{{{K_1}{K_2}{a^2}{\varepsilon _0}}}{{\left( {{K_1} - {K_2}} \right)}}\left( {\ln \left| {\dfrac{{{K_1}}}{{{K_2}}}} \right|} \right)$.

Note: Many students are confused as to why the given capacitor is considered as two capacitors connected in series, not in parallel. Well, look at the following figure to clear confusion.

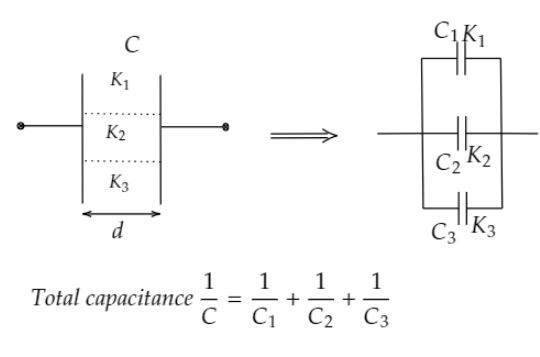
If a capacitor of capacitance $C$ filled with dielectrics of dielectric constant ${K_1}$, ${K_2}$, ${K_3}$ as shown in the above figure, then the original capacitor can be considered as three different capacitors connected in parallel. It is because the voltages across each dielectric are the same.

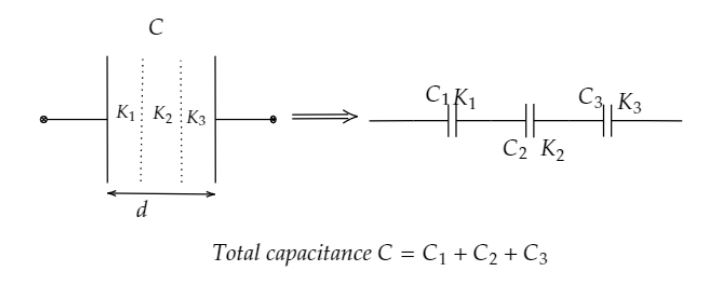
Now see the above figure. Since the voltages across each dielectric are different, the original capacitor can be considered as three different capacitors connected in series.