Question

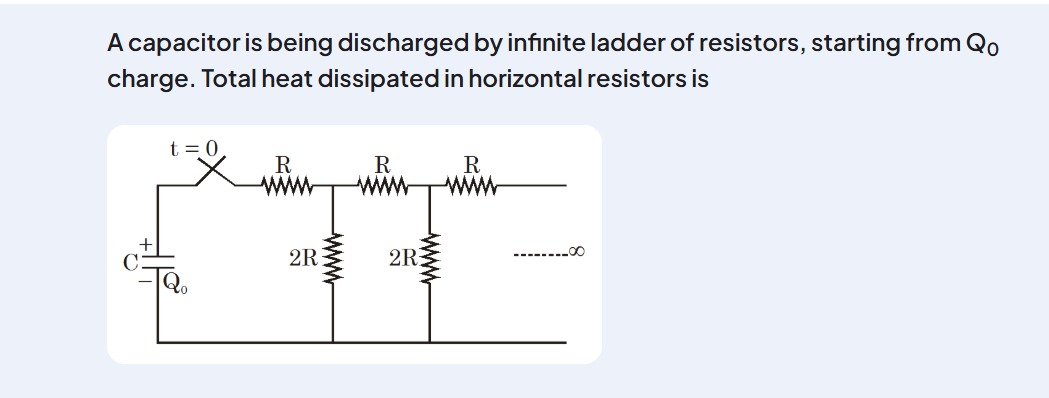
A capacitor is being discharged by infinite ladder of resistors, starting from $Q_0$ charge. Total heat dissipated in horizontal resistors is

Answer 1

$\frac{Q_0^2}{3RC}$

Answer 2

1. Equivalent Resistance: The infinite ladder network has an equivalent resistance $R_{eq}$ that can be found by setting up the equation: $R_{eq} = R + \frac{2R \cdot R_{eq}}{2R + R_{eq}}$ Solving this equation gives $R_{eq} = 2R$.

2. Discharge Current: The capacitor discharges through the equivalent resistance $R_{eq} = 2R$. The initial current is $I_0 = \frac{Q_0}{C R_{eq}} = \frac{Q_0}{2RC}$. The current at time $t$ is $I(t) = I_0 e^{-t/\tau}$, where $\tau = C R_{eq} = 2RC$.

3. Current in Horizontal Resistors: Let $I_n(t)$ be the current through the $n$-th horizontal resistor. Due to the ladder structure, the current through each successive horizontal resistor is halved: $I_n(t) = \left(\frac{1}{2}\right)^{n-1} I(t)$

4. Heat Dissipation in a Single Horizontal Resistor: The heat dissipated in the $n$-th horizontal resistor ($H_n$) is given by: $H_n = \int_0^\infty I_n(t)^2 R dt = \int_0^\infty \left[\left(\frac{1}{2}\right)^{n-1} I(t)\right]^2 R dt$ $H_n = \left(\frac{1}{4}\right)^{n-1} \int_0^\infty I(t)^2 R dt$ The integral $\int_0^\infty I(t)^2 R dt$ represents the total heat dissipated in the first horizontal resistor ($H_1$). $H_1 = \int_0^\infty \left(\frac{Q_0}{2RC} e^{-t/(2RC)}\right)^2 R dt = \left(\frac{Q_0}{2RC}\right)^2 R \int_0^\infty e^{-t/(RC)} dt$ $H_1 = \frac{Q_0^2}{4R^2C^2} R \left[-\frac{RC}{1} e^{-t/(RC)}\right]_0^\infty = \frac{Q_0^2}{4RC} (0 - (-RC)) = \frac{Q_0^2}{4RC}$ Therefore, $H_n = \left(\frac{1}{4}\right)^{n-1} \frac{Q_0^2}{4RC}$.

5. Total Heat Dissipated: The total heat dissipated in all horizontal resistors is the sum of $H_n$ from $n=1$ to $\infty$: $H_{total\_horizontal} = \sum_{n=1}^{\infty} H_n = \sum_{n=1}^{\infty} \left(\frac{1}{4}\right)^{n-1} \frac{Q_0^2}{4RC}$ This is a geometric series with the first term $a = \frac{Q_0^2}{4RC}$ and common ratio $r = \frac{1}{4}$. The sum is $S = \frac{a}{1-r} = \frac{\frac{Q_0^2}{4RC}}{1 - \frac{1}{4}} = \frac{\frac{Q_0^2}{4RC}}{\frac{3}{4}} = \frac{Q_0^2}{3RC}$.