Question

A capacitor ${C_1} = 1\,\mu F$ is charged up to a voltage $V = 60\,V$ by connecting it to a battery $B$ through the switch $\left( 1 \right)$. Now ${C_1}$ is disconnected from battery and connected to a circuit consisting of two uncharged capacitors ${C_2} = 3\,\mu F$ and ${C_3} = 6\,\mu F$ through a switch $\left( 2 \right)$ as shown in the figure. The sum of final charges an ${C_2}$ and ${C_3}$ is:

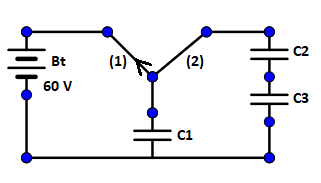
(A) $40\,\mu C$
(B) $36\,\mu C$
(C) $20\,\mu C$
(D) $54\,\mu C$

Answer 1

The sum of the final charges an ${C_2}$ and ${C_3}$ can be determined by using two formulas. The capacitor is series formula and then the potential difference in capacitor formula. By using the given information in these two formulas, the sum of final charges ${C_2}$ and ${C_3}$ can be determined.

Formulae Used:
Capacitor in series,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
Where, $C$ is the equivalent capacitance, ${C_1}$ capacitance of the first capacitor and ${C_2}$ is the capacitance of the second capacitor.
Potential difference in capacitor,
$V = \dfrac{Q}{C}$
Where, $V$ is the potential difference, $Q$ is the charge and $C$ is the capacitance.

Complete step-by-step solution:
Given that,
A capacitor, ${C_1} = 1\,\mu F$
Voltage $V = 60\,V$
The capacitance is, ${C_2} = 3\,\mu F$ and ${C_3} = 6\,\mu F$
Capacitor in series, and the capacitors ${C_2}$ and ${C_3}$ are in series then,
$\dfrac{1}{C} = \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}\,..................\left( 1 \right)$
By rearranging the terms, then the above equation is written as,
$\dfrac{1}{C} = \dfrac{{{C_3} + {C_2}}}{{{C_3} \times {C_2}}}$
By taking reciprocal on both sides of the above equation, then the above equation is written as,
$C = \dfrac{{{C_3} \times {C_2}}}{{{C_3} + {C_2}}}$
By substituting the terms given terms in the above equation, then
$C = \dfrac{{6 \times 3}}{{6 + 3}}$
On further simplification, then
$C = \dfrac{{18}}{9}$
On dividing, then the above equation is written as,
$C = 2\,\mu F$
Now, the potential difference across three capacitors ${C_1}$ and $C$ (Here $C$ is the combined capacitance of ${C_2}$ and ${C_3}$ )
$V = \dfrac{Q}{{{C_1} + C}}$
By substituting the charge and the capacitance in the above equation, then
$V = \dfrac{{60}}{{1 + 2}}$
On further simplification, then
$V = \dfrac{{60}}{3}$
On dividing the terms in the above equation, then
$V = 20\,V$
The sum of the charge of the capacitors ${C_2}$ and ${C_3}$ are,
$Q = C \times V$ (Here $C$ is the combined capacitance of ${C_2}$ and ${C_3}$ )
Now, substituting the combined capacitance of ${C_2}$ and ${C_3}$, and the potential difference $V$ in the above equation, then
$Q = 2 \times 20$
On multiplying, then
$Q = 40\,\mu C$
Thus, the above equation shows the sum of final charges ${C_2}$ and ${C_3}$.
Hence, the option (A) is correct.

Note:- The capacitors ${C_2}$ and ${C_3}$ are in series, so the capacitor in series formula is used. Then, we have to find the total charge across the second capacitor and the third capacitor, so the equivalent capacitance of ${C_2}$ and ${C_3}$ are multiplied with the potential difference.