Question
Question: A capacitor and resistor are connected with an AC source as shown in figure. The capacitor is \({X_C...
A capacitor and resistor are connected with an AC source as shown in figure. The capacitor is XC=3Ω and resistance of the resistor is4Ω. Phase difference between current I andI1 is [tan−1(43)=37∘] :
A. 90∘
B. Zero
C. 53∘
D. 37∘
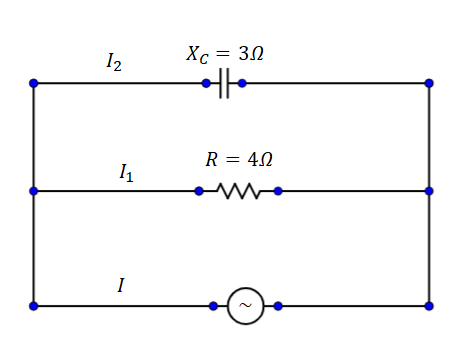
Solution
Hint:- The resultant of the capacitor resistance and the resistance of the resistor will give us the total resistance of the circuit. The current in the capacitor and in the resistor will be different as the resistance of the two elements are also different.
Formula used: The formula of the ohm's law is given by, V=I⋅R where V is the potential difference. I is the current in the circuit and R is the resistance in the circuit.
Complete step-by-step solution
Since the ohm's law is given byV=I⋅R.
Where V is the potential difference. I is the current in the circuit and R is the resistance in the circuit.
The current passing through the capacitor can be calculated by,
⇒V=I2⋅(Xc)
Here Xc is the reactance of the capacitor and V isVrms.
⇒I2=XcV
Replace the value of reactance of the capacitor, XC=3Ω.
⇒I2=3V.
The current of the capacitor is equal to I2=3V.
The current flowing in the resistor of resistance of 4Ω is equal to,
⇒I=RV
⇒I=4V
The current flowing through the resistor of resistance 4Ω is equal to I=4V.
The current I2 is 90∘ ahead of the applied voltage and the current I is in the same phase therefore the phase difference between I andI2.is given by,
⇒tanϕ=II2
⇒tanϕ=(4V)(3V)
⇒tanϕ=34.
⇒ϕ=tan−1(34)
⇒ϕ=53∘.
The phase difference between current I andI2.is equal toϕ=53∘. The correct answer for this problem is option C.
Note:- The resistance offered by the capacitor in the dc circuit is infinite because the resistance offered by the capacitor is inversely proportional to the angular frequency of the circuit and the angular frequency in the dc circuit is zero.
