Question

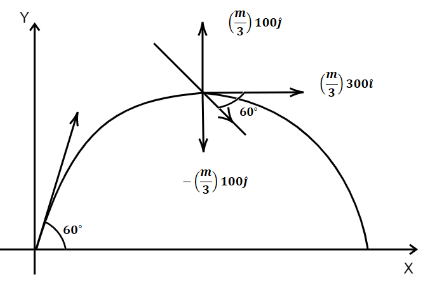
A cannonball is fired with velocity $200\,m{s^{ - 1}}$ at an angle of ${60^ \circ }$ with the horizontal. At the highest point of its flight, it explodes into 3 equal fragments, one going vertically upwards with a velocity $100\,m{s^{ - 1}}$, the second one fallings vertically downwards with a velocity $100\,m{s^{ - 1}}$. The third fragment will be moving with a velocity
A. $100\,m{s^{ - 1}}$ in the horizontal direction f
B. $300\,m{s^{ - 1}}$ in the horizontal direction
C. $300\,m{s^{ - 1}}$ in a direction making an angle ${60^ \circ }$ with the horizontal
D. $200\,m{s^{ - 1}}$ in a direction making an angle ${60^ \circ }$ with the horizontal

Answer 1

Use the conservation of momentum at the point of explosion and find the velocity of the ball at that point. From there find the velocity of the third fragment. The conservation of momentum states that the momentum at any instant of time is conserved when no external force is applied to the system.

Formula used:
The velocity along X axis of a projectile is given by,
${v_x} = u\cos \theta$
where, $u$ is the initial velocity and $\theta$ is the angle of projection.
The conservation of momentum is given by,
$mv = K$
where, $K$ is some constant and $mv$ is the momentum of the body.

Complete step by step answer:
We have given here a cannonball which explodes at the highest point into three equal parts. Now, at the highest point of it motion the velocity along the vertical is zero and we know the velocity along horizontal is constant and is given by,
${v_x} = u\cos \theta$

So, the velocity of the cannonball before explosion will be,

\Rightarrow V = 100\hat i\,m{s^{ - 1}}$$. The velocity of the fragment going vertically upwards is $$100\hat j\,m{s^{ - 1}}$$ and the velocity of the fragment going vertically downwards $$ - 100\hat j\,m{s^{ - 1}}$$. Now, let the mass be $$m$$. And let the velocity of the third fragment be $$\vec Am{s^{ - 1}}$$ Hence, from conservation of momentum we can write, $$\dfrac{m}{3}100\hat j - \dfrac{m}{3}100\hat j\, + \dfrac{m}{3}\vec A = m100\hat i$$ $$\dfrac{m}{3}\vec A = m100\hat i$$ $$\therefore \vec A = 300\hat i$$ Hence, the velocity of the third fragment will be along the positive X axis. Now, the fragments are at some height. Hence, the third fragment will make the same angle as the angle of projection means $${60^ \circ }$$ and after the explosion it will come back to the ground with the same angle since it has some velocity along the horizontal axis. Hence, the third fragment will move with a velocity of $$300\,m{s^{ - 1}}$$ in a direction making an angle of $${60^ \circ }$$ with the horizontal. **Hence, option C is the correct answer.** **Note:** Remember that since only the direction of the velocity is only in the positive X direction does not mean that it will move along the X axis. Since, the particles are at a height the gravity will pull them vertically downwards also so along with the horizontal velocity it will also have a vertical velocity which will make the angle $${60^ \circ }$$ with the horizontal.