Question

A cannon on the level plane is aimed at an angle $\theta$ above the horizontal and a shell is fired with a muzzle velocity ${{V}_{0}}$​ towards the vertical cliff at a distance $R$ away. The height from the bottom at which the shell hits the side walls of the cliff is given as,
$\begin{aligned} & A.R\tan \theta -\dfrac{g{{R}^{2}}}{2{{V}_{0}}^{2}{{\cos }^{2}}\theta } \\\ & B.R\tan \theta -\dfrac{g{{R}^{2}}}{2{{V}_{0}}^{2}} \\\ & C.R\tan \theta -\dfrac{g{{R}^{2}}}{2{{V}_{0}}^{2}{{\sin }^{2}}\theta } \\\ & D.R\tan \theta +\dfrac{g{{R}^{2}}}{2{{V}_{0}}^{2}{{\cos }^{2}}\theta } \\\ \end{aligned}$

Answer 1

In the horizontal direction, the acceleration is found to be zero. Only acceleration is there in the vertical direction. This value of acceleration and the height at which the shell hits are applied in Newton's second equation of motion. These all may help you to solve this question.

Complete step by step answer:
For the horizontal direction, we can write that,
$u=v\cos \theta$
And also the acceleration in the horizontal direction is found to be zero.
Therefore we can write that,
For the vertical direction we can write that the velocity will be,
$u=v\sin \theta$
And the acceleration will be $g$,
Therefore applying this in the newton’s second equation of motion,
Let us eliminate the $t$ from both the equations, so that we can write,
$y\left( t \right)=v\sin \theta \times \dfrac{x\left( t \right)}{v\cos \theta }-\dfrac{1}{2}g{{\left( \dfrac{x\left( t \right)}{v\cos \theta } \right)}^{2}}$
Now let us substitute the values given in the question,
Angle above the horizontal is given as,
$\theta =\theta$
The muzzle velocity is given as,
$v={{V}_{0}}$
The range of the projectile motion is substituted as,
$x\left( t \right)=R$
And the height of the projectile is given as,
$y\left( t \right)=H$
Substituting all these in the above obtained equation will give,
$H={{V}_{0}}\sin \theta \times \dfrac{R}{{{V}_{0}}\cos \theta }-\dfrac{1}{2}g{{\left( \dfrac{R}{{{V}_{0}}\cos \theta } \right)}^{2}}$
Simplifying the obtained equation by cancelling the common terms will give,
$H=R\tan \theta -\left( \dfrac{g{{R}^{2}}}{2{{V}_{0}}^{2}{{\cos }^{2}}\theta } \right)$
Therefore the best possible answer is obtained.

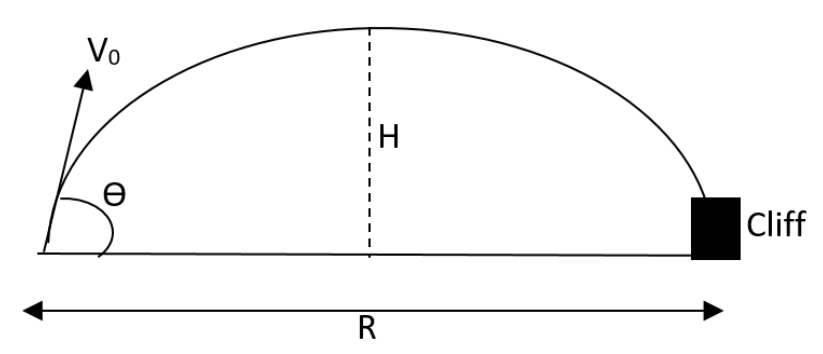
So, the correct answer is “Option A”.

Note: If the projectile is at a vertical velocity which is zero, then the height is known as the maximum height of the projectile. After this the gravity will take over and accelerate the body downwards. The displacement of the projectile in the horizontal direction is known as the range of the projectile. It is dependent on the initial velocity of the body.