Question

A cannon on a level plane is aimed at an angle $\theta$ above the horizontal and a shell is fired with a muzzle velocity ${{v}_{0}}$ towards a vertical cliff a distance D away. Then the height from the bottom at which the shell strikes the side wall of the cliff is –

& A)\text{ Dsin}\theta -\dfrac{g{{D}^{2}}}{2v_{0}^{2}{{\sin }^{2}}\theta } \\\ & B)\text{ Dcos}\theta -\dfrac{g{{D}^{2}}}{2v_{0}^{2}co{{\operatorname{s}}^{2}}\theta } \\\ & C)\text{ Dtan}\theta -\dfrac{g{{D}^{2}}}{2v_{0}^{2}{{\cos }^{2}}\theta } \\\ & D)\text{ Dtan}\theta -\dfrac{g{{D}^{2}}}{2v_{0}^{2}{{\sin }^{2}}\theta } \\\ \end{aligned}$$

Answer 1

We are discussing a projectile motion of a shell being fired with a muzzle velocity $v_{0}^{{}}$from a horizontal plane to a cliff at a distance D from the canon. We need to apply the equations of motion to determine the height at which the shell hits the cliff.

Complete answer:
Let us understand the situation given in the question. A projectile motion of a cannon shell is to be analysed here. The following figure describes the event by resolving the velocity along the horizontal and vertical axes.

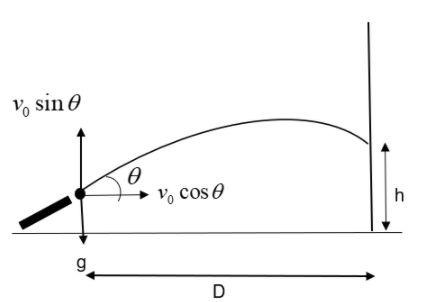
From the figure, it is clear that the height h from the bottom can be measured by using the equations of motion
$S=ut+\dfrac{1}{2}a{{t}^{2}}$.
For that, let us consider the distance travelled along each of the axes.
Along x-axis the acceleration is zero,
$x(t)={{v}_{0}}\cos \theta .t$ ---(1)
is the distance due to the horizontal velocity ${{v}_{0}}\cos \theta$ in time t.
Along the y-axis,
$y(t)={{v}_{0}}\sin \theta .t-\dfrac{1}{2}g{{t}^{2}}$ ---(2)
We realise that along the vertical direction the gravitational force also acts which causes a vertical acceleration in the opposite direction as that of the vertical velocity.
Now let us remove the time variable by substituting (1) in (2)

& t=\dfrac{x(t)}{{{v}_{0}}\cos \theta } \\\ & \Rightarrow y(t)={{v}_{0}}\sin \theta .(\dfrac{x(t)}{{{v}_{0}}\cos \theta })-\dfrac{1}{2}g{{(\dfrac{x(t)}{{{v}_{0}}\cos \theta })}^{2}} \\\ \end{aligned}$$ We know that the horizontal distance travelled is D, i.e., $$x(t)=D$$ and $$y(t)=h$$, $$\begin{aligned} & \Rightarrow y(t)={{v}_{0}}\sin \theta .(\dfrac{D}{{{v}_{0}}\cos \theta })-\dfrac{1}{2}g{{(\dfrac{D}{{{v}_{0}}\cos \theta })}^{2}} \\\ & \Rightarrow h=y(t)=\dfrac{D}{\tan \theta }-\dfrac{g{{D}^{2}}}{2v_{0}^{2}{{\cos }^{2}}\theta } \\\ \end{aligned}$$ So, the height from bottom where the cannon shell hits the cliff is – $$h=\dfrac{D}{\tan \theta }-\dfrac{g{{D}^{2}}}{2v_{0}^{2}{{\cos }^{2}}\theta }$$ **The correct answer is option C.** **Additional Information:** The height at which the shell strikes is the vertical distance of the shell at that point of the projectile. **Note:** In projectile motions, the angle plays an important role in determining the height of the projectile and the range of the projectile. A right-angled projectile results in the highest projectile, which will reduce to a one-dimensional motion. A $${{45}^{0}}$$ projectile results in the longest range or horizontal distance.