Question

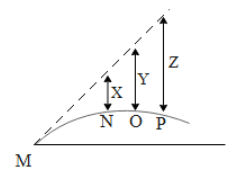
A cannon fires a projectile as shown in the figure below. The dashed line shows the trajectory in the absence of gravity. The points M , N, O and P correspond to time t= 1s, 2s and 3s respectively. The length of X, Y and Z respectively are:

a)5m, 10m 15m
b)10m, 40m, 90m
c)5m, 20m, 45m
d)10m, 20m, 30m

Answer 1

In the above figure the dotted line indicates the path traversed by the cannon ball in the absence of gravity and the curved path represents the path traversed in the presence of gravity. The height attained by the ball in either case depends on the initial vertical component of velocity. Hence using Newton’s second kinematic equation we will determine the distance X, Y and Z by taking the difference in the vertical distance between the cannon balls along two different paths.
Formula used:
$S=Ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
Let us say the cannonball is fired at initial velocity U. At any of instant time t the distance(S) covered by the ball under acceleration ‘a ‘is given by,
$S=Ut+\dfrac{1}{2}g{{t}^{2}}$
Let us say the ball is projected with initial velocity $USin\theta$ where $\theta$ is the angle between the initial velocity with respect to ground. Hence the vertical distance (${{S}_{g}}$) covered by the ball in the presence of acceleration due to gravity(g),
${{S}_{g}}=USin\theta t-\dfrac{1}{2}g{{t}^{2}}$
The vertical distance(${{S}_{0}}$ ) covered by the ball in the absence of gravity is equal to,
$\begin{aligned} & {{S}_{0}}=USin\theta t+\dfrac{1}{2}0{{t}^{2}} \\\ & \Rightarrow {{S}_{0}}=USin\theta t \\\ \end{aligned}$
Hence the distance between the same ball along two different paths at different instant of time i.e. D(t)
is given by,
$\begin{aligned} & D(t)={{S}_{0}}-{{S}_{g}}=USin\theta t-USin\theta t-\dfrac{1}{2}g{{t}^{2}} \\\ & D(t)=-\dfrac{1}{2}g{{t}^{2}} \\\ & At\text{ t=1s, }D(1)=X \\\ & \Rightarrow X=\dfrac{1}{2}10{{(1)}^{2}}=5m \\\ & At\text{ t=2s, }D(2)=Y \\\ & \Rightarrow Y=\dfrac{1}{2}10{{(2)}^{2}}=20m \\\ & At\text{ t=3s, }D(3)=Z \\\ & \Rightarrow Y=\dfrac{1}{2}10{{(3)}^{2}}=45m \\\ \end{aligned}$

Hence the correct answer of the above question is option c.

Note:
It is to be noted that the horizontal component of the initial velocity remains constant in both the above cases. Hence the two balls along different paths remain along the same vertical line at any instant of height. It is also to be noted that the above scenario only holds true in vacuum.