Question

A sector cut from a uniform disk of radius 12 cm and a uniform rod of the same mass bent into shape of an arc are arranged facing each other as shown in the figure. If center of mass of the combination is at the origin, what is the radius of the arc?

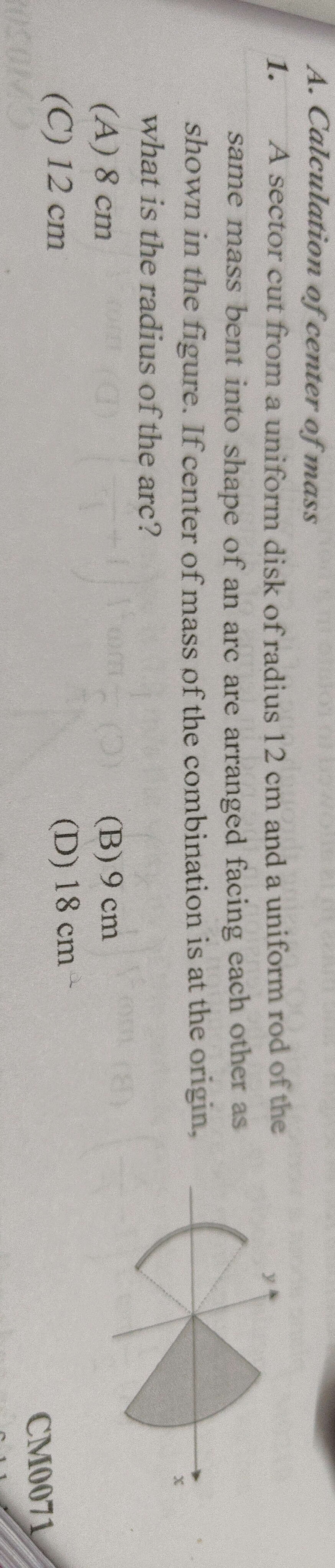
• A. 8 cm
• B. 9 cm
• C. 12 cm
• D. 18 cm

Answer 1

Answer: (A)

8 cm

Answer 2

The problem involves finding the radius of a semi-circular arc such that its combination with a semi-circular sector of a disk has its center of mass at the origin. Both components are stated to be uniform and have the same mass.

1. Identify the components and their properties:

• Component 1: Sector cut from a uniform disk.

  • Shape: Appears to be a semi-circular disk (angle $\pi$ or 180 degrees).
  • Radius: $R_S = 12$ cm.
  • Mass: Let $M_S = M$.

• Component 2: Uniform rod bent into the shape of an arc.

  • Shape: Appears to be a semi-circular arc (angle $\pi$ or 180 degrees).
  • Radius: Let $R_A = R$ (unknown).
  • Mass: Let $M_A = M$ (same mass as the sector).

2. Determine the center of mass (CM) for each component:

The figure shows the sector on the positive x-axis side and the arc on the negative x-axis side, with the origin at their common vertex/center. Both are symmetric about the x-axis, so their y-coordinates of CM will be 0. We only need to consider the x-coordinates.

• Center of mass of a uniform semi-circular disk of radius $R_S$:

  The CM is located at a distance $x_{CM,S}$ from the center along the axis of symmetry. The formula for a sector of angle $2\alpha$ is $\frac{2R_S \sin\alpha}{3\alpha}$. For a semi-circle, $2\alpha = \pi$, so $\alpha = \pi/2$. $x_{CM,S} = \frac{2R_S \sin(\pi/2)}{3(\pi/2)} = \frac{2R_S}{3\pi/2} = \frac{4R_S}{3\pi}$. Given $R_S = 12$ cm: $x_{CM,S} = \frac{4 \times 12}{3\pi} = \frac{48}{3\pi} = \frac{16}{\pi}$ cm. Since the sector is on the positive x-side, its CM is at $(\frac{16}{\pi}, 0)$.

• Center of mass of a uniform semi-circular arc of radius $R_A$:

  The CM is located at a distance $x_{CM,A}$ from the center along the axis of symmetry. The formula for an arc of angle $2\alpha$ is $\frac{R_A \sin\alpha}{\alpha}$. For a semi-circle, $2\alpha = \pi$, so $\alpha = \pi/2$. $x_{CM,A} = \frac{R_A \sin(\pi/2)}{\pi/2} = \frac{R_A}{\pi/2} = \frac{2R_A}{\pi}$. Since the arc is on the negative x-side, its CM is at $(-\frac{2R_A}{\pi}, 0)$. Let $R_A = R$. So, its CM is at $(-\frac{2R}{\pi}, 0)$.

3. Calculate the center of mass of the combination:

The x-coordinate of the center of mass of the combination ($X_{CM}$) is given by: $X_{CM} = \frac{M_S x_{CM,S} + M_A x_{CM,A}}{M_S + M_A}$

We are given that the center of mass of the combination is at the origin, so $X_{CM} = 0$. Also, $M_S = M_A = M$.

$0 = \frac{M \left(\frac{16}{\pi}\right) + M \left(-\frac{2R}{\pi}\right)}{M + M}$ $0 = \frac{M \left(\frac{16}{\pi} - \frac{2R}{\pi}\right)}{2M}$

Since $M \neq 0$, we can cancel $M$ from the numerator and denominator: $0 = \frac{1}{2} \left(\frac{16 - 2R}{\pi}\right)$

For this equation to be true, the numerator must be zero: $16 - 2R = 0$ $2R = 16$ $R = 8$ cm

Thus, the radius of the arc is 8 cm.