Question
Question: A.Calculate the torque with which the wheel is turning . 
B. Which wheel will have more turning effect and why?
i.
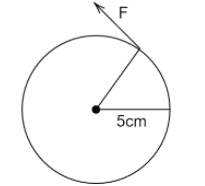
ii.
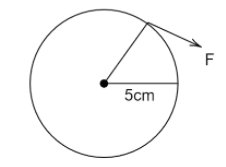
iii.
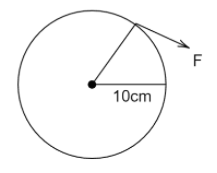
Solution
The amount of force required to twist an object is measured by torque. For part (A) torque can be found out by the relation between force, radius, and angle between force and lever arm. For part (B) find the individual torque for all three wheels then compare which will have more turning effect.
Complete answer:
Solution of the part (A) -
We have been given the radius of the wheel R=5cm=0.05m and force acting on the wheel is F=10N
The amount of force required to twist an object is measured as torque which is given as
τ=RFsinθ
Where θ is the angle between force and lever arm.
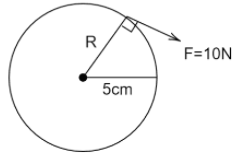
⇒τ=0.05×10×sin90∘
⇒τ=0.5Nm
Hence the torque with which the wheel is turning is τ=0.5Nm
Solution for part (B)- turning effect depends upon, force, the shortest distance between the force line and axis of rotation.
i.

Dividing the given force into its components. Taking the cosθ component of force which is making the tangent with the wheel. Torque for the given wheel will be
⇒τ=RFcosθ
⇒τ=0.05Fcosθ
ii.

torque for the given wheel is
τ=0.05F
iii.
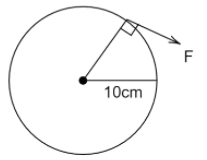
Here radius R=10cm=0.10m therefore, torque for the given wheel is
τ=0.10F
So, the turning effect on the wheel will be like (iii) > (ii) >(i)
Hence, torque is found to be maximum in wheel given in (iii) therefore, wheel in the (iii) option will have more turning effect.
Note:
A straight line that only touches the circle once is a tangent to a circle. It is called the point of tangency. At this point, the tangent to a circle is always perpendicular to the radius that is why we took θ=90∘ here.
