Question

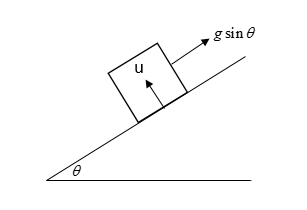
A cabin is moved up the inclined plane with a constant acceleration $g\sin \theta$. A particle is projected with some velocity with respect to the cabin in the direction perpendicular to the inclined plane. If the maximum height attained by a particle perpendicular to the inclined plane is the same as the range of particles with respect to the cabin parallel to the plane then calculate values of $\cot \theta$.

Answer 1

Hint
First we need to consider the origin to be placed in the cabin and at the position from where the particle is projected. Then we need to divide the velocity into components parallel and perpendicular to the inclined plane. Then we need to find the resultant x and y components of the displacement. At last, we need to equate the respective equations and solve them to get the final equation.
$displacement = velocity \times time$
$S = ut + \dfrac{1}{2}g{t^2}$
Where, $S$ is displacement, $u$ is velocity, $t$ is time and $g$ is gravity

Complete step by step answer
In the problem, it is mentioned that the cabin is moved up the inclined plane with a constant acceleration$g\sin \theta$. Let's assume that the instantaneous velocity of the cabin travelling upward is ${u_1}$.Let's consider that the origin is set at the position from where the particle has been thrown upward perpendicularly to the inclined plane as shown in the image and its velocity is ${u_2}$. Now, we can draw the components of the velocity as follows:

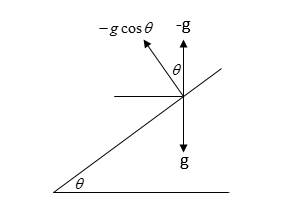
Visually we can conclude,
Deceleration of the particle in the direction perpendicular to the inclined plane = $- g\cos \theta$(negative sign to indicate the opposite direction of gravitational force).
Time to reach the maximum height perpendicular to the plane =$\dfrac{{velocity}}{{g\cos \theta }} = \dfrac{{{u_2}}}{{g\cos \theta }}$
The maximum height perpendicular to the plane = $\dfrac{{{{(velocity)}^2}}}{{2g\cos \theta }} = \dfrac{{{u_2}^2}}{{2g\cos \theta }}$
Displacement in the x-direction = $x$ = $\left( {velocity{\text{ }}of{\text{ }}cabin{\text{ }}or{\text{ }}origin{\text{ }}in{\text{ }}x - direction{\text{ }}-{\text{ }}velocity{\text{ }}of{\text{ }}the{\text{ }}particle{\text{ }}in{\text{ }}the{\text{ }}x - direction} \right) \times \left( {time} \right)$= $({u_1}\cos \theta - {u_2}\sin \theta ) \times t$ (here, $t$ indicated the time) ($\because displacement = velocity \times time$)
Displacement in the y-direction = $y$ =

\left[ {\\{ \left( {velocity{\text{ }}of{\text{ }}cabin{\text{ }}or{\text{ }}origin{\text{ }}in{\text{ }}y - direction){\text{ + (}}velocity{\text{ }}of{\text{ }}the{\text{ }}particle{\text{ }}in{\text{ }}the{\text{ }}y - direction} \right)\\} \times \left( {time} \right)} \right] \\\ \+ \dfrac{1}{2}g{(time)^2} \\\ $$= $({u_1}\sin \theta + {u_2}\cos \theta )t - \dfrac{1}{2}g{t^2}$ For the ball to meet the inclined floor we can write = $y$ = $$\;x(tan\theta )$$ We can substitute the value of $y$ and we get = $$t{\text{ }} = {\text{ }}\dfrac{{\left( {2{\text{ }}{u_2}{\text{ }}Sec\;\theta } \right)}}{g}$$ After equating relative maximum height and range we can get, $\dfrac{{{u_2}^2}}{{(2gcos\theta )}} = ({u_2}tan\theta + \dfrac{g}{{2Sin\theta }} \times \dfrac{{2{u_2}sec\theta }}{g})(\dfrac{{2{u_2}sec\theta }}{g})$ By Simplifying the above equation we get, $\cot \theta = 8$ The value of the $\cot \theta $ is 8. **Note** When dividing the velocity into components we need to be careful about the value of the angle that the velocity is making with the plane of interest. We need to look for the proper plane about which we need to resolve the velocity components. Choosing the wrong plane will complicate the solution and might lead to catastrophe.