Solveeit Logo
Login

Question

Question: A bullet travels horizontally at \[660m{{s}^{-1}}\]at a height of 5m from a man. The distance (in m)...

A bullet travels horizontally at 660ms−1660m{{s}^{-1}}at a height of 5m from a man. The distance (in m) is the bullet from the man when he hears its whistle is (10+x). Find x. Velocity of sound in air=340ms−1340m{{s}^{-1}} (Round off the answer to the nearest integer)

Explanation

Solution

Hint: The basic theory and formula used in this question belongs to motion. We just have to recall the formula containing the relation between distance, speed and time. The formula which is going to be used in this question is, distance is equal to velocity times time i.e. d=v×td=v\times t. This question also requires the basic knowledge of the Doppler effect of sound which comes inside the topic of waves.

Complete step by step answer:
At the instant t = 0, the bullet is at its initial point O form where the man heard the whistle of the bullet. The time taken by the sound to reach the man at point A be t sec, during this time the bullet reaches at any point B.

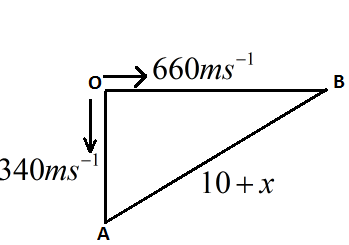
We have to calculate the distance of AB.
Here,
Velocity of sound vs=340ms−1{{v}_{s}}=340m{{s}^{-1}}
Thus, by using the formula,

& d=v\times t \\\ & 5=340t \\\ & t=\dfrac{5}{340} \\\ \end{aligned}$$ Also, velocity of bullet $${{v}_{b}}=660m{{s}^{-1}}$$ So in time t bullet travels, $$\begin{aligned} & d=v\times t \\\ & d=660t \\\ & d=660\times \dfrac{5}{340} \\\ & d=9.7m \\\ \end{aligned}$$ Now, the distance between the bullet and the man is AB which is given by: $$\begin{aligned} & A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}} \\\ & AB=\sqrt{{{5}^{2}}+{{9.7}^{2}}}=\sqrt{119.09} \\\ & AB=10.9m \\\ \end{aligned}$$ Comparing this distance with (10+x) we will find the value of x. $$\begin{aligned} & 10+x=10.9 \\\ & x=0.9 \\\ \end{aligned}$$ We have to round off this answer to the nearest integer i.e. the value of x=1. Note: The common mistake done by the students in this question is that they keep the value at distance as 5m but sometimes they take the value of speed of bullet instead of sound which will make the solution completely wrong. Also the process of finding the value of x by putting (10+x) instead of x in the solution will not make the solution wrong, but it will just make the calculation of the solution lengthier.