Question

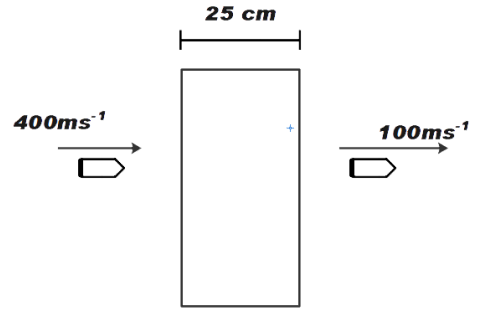
A bullet of mass 5g moving with velocity 400 $m{{s}^{-1}}$ trikes a wall of thickness 25 cm and goes out of the other side with a velocity of 100 $m{{s}^{-1}}$. Calculate the opposition force offered by the wall.

Answer 1

In this question, we have been asked to calculate the force offered by the wall to the moving bullet. We know that force is mass times acceleration. We have been given the mass of the bullet. Therefore, we will calculate the acceleration of the bullet. We will be using the equation of motion to calculate the acceleration.

Formula used: - ${{v}^{2}}={{u}^{2}}+2as$
Where,
v is the final velocity in $m{{s}^{-1}}$
u is the initial velocity in $m{{s}^{-1}}$
s is the distance travelled in meters
a is the acceleration in $m{{s}^{-2}}$

Complete answer:
We know that a bullet is moving with velocity 400 $m{{s}^{-1}}$, this is the initial velocity and final velocity is given as 100 $m{{s}^{-1}}$. The thickness of the wall is 25 cm i.e. 0.25 m. This is the distance travelled by the bullet.

                 ![](https://www.vedantu.com/question-sets/5c2898db-fa63-4a99-806c-be7c8948fe974345673447288579752.png)   

Now, we know from the 3rd equation of motion
${{v}^{2}}={{u}^{2}}+2as$
After substituting the given values
We get,
${{100}^{2}}={{400}^{2}}+2\times a\times 0.25$
On solving,
We get,
$a=\dfrac{{{100}^{2}}-{{400}^{2}}}{2\times 0.25}$
Therefore,
$a=-300000m{{s}^{-2}}$
The negative sign of acceleration represents the retardation. Since, the force is opposition force we will be neglecting the negative sign for calculation of force.
Now using the calculated retardation, to calculate force we are given the mass as 25g i.e. 0.025kg
We know,
F = ma
F = $0.025\times 300000m{{s}^{-2}}$
Therefore,
F = 7500 N
This can also be written as,
F = 7.5 kN
Therefore, the correct answer is 7.5 kN.

Note:
If the acceleration is constant, there are three laws that define the motion of a body. These laws are called laws of motion. However, these laws are applicable only to macro systems. It means that these laws of motion when applied to quantum mechanics. The three laws of motion are as follows,
$v=u+at$
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
${{v}^{2}}={{u}^{2}}+2as$