Solveeit Logo
Login

Question

Question: A bullet of mass 50 g moving with velocity 200 m/s penetrates a wooden block of mass 5 kg suspended ...

A bullet of mass 50 g moving with velocity 200 m/s penetrates a wooden block of mass 5 kg suspended through a string from rigid support and comes to rest inside it. If the length of the string is 10 m find the angular deflection of the string.

Explanation

Solution

Using the conservation of momentum, we equate the momentum before and after collision, when the bullet moves in the block. Hence, the mass of the system after bullet lodges itself in the block it becomes:
u=m+Mmu=\dfrac{m+M}{m}
To find the velocity of the block we will equate the linear momentum of the bullet and block(stationary) to the momentum of the block when the bullet has pierced it.
mv+Mu=(m+M)Vmv+Mu=(m+M)V

We also use the law of conservation of energy to find the height the block moves:
12(m+M)v2=(m+M)gh\dfrac{1}{2}\left( m+M \right){{v}^{2}}=\left( m+M \right)gh
Now after finding the value h, we need to find the value of the angle using the formula:
h=l(1−cos⁡θ)h=l\left( 1-\cos \theta\right)
where m is the mass of the bullet, M is the mass of the bullet, v is the velocity of the bullet, V is the velocity of the block after being hit by the bullet, h is the height raised from original position to a certain position at a certain angle θ and \l\ is the length of the string.

Complete step by step answer:
The mass and velocity system for the bullet before hitting the block with mass of the bullet as 50g and a velocity of v=200m/sv=200m/s gives the linear momentum as mv as:
501000kg×200m/s=10kgm/s\dfrac{50}{1000}kg\times 200m/s=10kgm/s…(1)

The mass and velocity system for the bullet after hitting the block of \5kg\ with mass of the bullet as 50g and a velocity of v=200m/sv=200m/s gives the linear momentum as mv as:
5kg×05kg\times 0 with v=0v=0 as the block is stationary.…(2)

The momentum of the block after the bullet is in the block and swings with a certain velocity V is given as:
(m+M)V\left( m+M \right)V
⇒(501000+5)V\Rightarrow \left( \dfrac{50}{1000}+5 \right)V
⇒(5.05)V\Rightarrow \left( 5.05 \right)V…(3)

Now adding the equation (1) and (2) as both are events before bullet hits the block and equating them with equation (3) as:
10+5×0=(5.05)V10+5\times 0=\left( 5.05 \right)V
⇒V=105.05\Rightarrow V=\dfrac{10}{5.05}
⇒V=1.98m/s\Rightarrow V=1.98m/s

Now as we know the velocity of the block after the bullet hits the block is given then we can proceed with finding the distance h as shown below in the diagram to find the potential energy of the block after reaching the top of the arc.

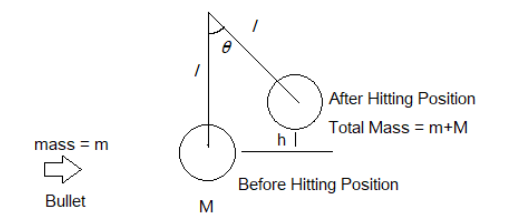
Now to find the height h, we equate the kinetic energy of the bullet and the potential energy of the block after hitting the bullet at a ‘h’ distance from the base position.
Hence, 12mV2=mgh\dfrac{1}{2}m{{V}^{2}}=mgh
Placing the values in the above formula we get the value of h as:
h=12V2gh=\dfrac{1}{2}\dfrac{{{V}^{2}}}{g}
With gravity as g=10m/s2g=10m/{{s}^{2}}, we get the height raised as:
h=12×3.9210h=\dfrac{1}{2}\times \dfrac{3.92}{10}
h=0.196mh=0.196m

Now using the radius to arc formula we get the angle rotated till height h as:
h=l(1−cos⁡θ)h=l\left( 1-\cos \theta\right)
Placing the value of h=0.196mh=0.196m and l=10ml=10m
⇒cos⁡θ=10−1.9610\Rightarrow \cos \theta =\dfrac{10-1.96}{10}
⇒cos⁡θ=10−1.9610\Rightarrow \cos \theta =\dfrac{10-1.96}{10}
⇒θ=cos⁡−1(0.98)\Rightarrow \theta ={{\cos }^{-1}}\left( 0.98 \right)
⇒θ=11.38∘\Rightarrow \theta ={{11.38}^{\circ }}
Therefore, the angular deflection is 11.38∘{{11.38}^{\circ }}.

Note: The above example of bullet and block pendulum uses the conservation of momentum to find the velocity of the block when hit by the bullet and not conservation of energy as before reaching the destined point the energy is not conserved and is transformed into an immeasurable form i.e. Internal Energy. Hence to find the velocity we use the conservation of momentum and to find the height the block reaches after hit we use conservation of energy.