Question

A bullet of mass $25kg$ is fired horizontally into a ballistic pendulum of mass $5kg$ and gets embedded in it. If the center of the pendulum rises by a distance $10cm$, find the speed of the bullet.

Answer 1

We have studied the law of conservation of energy and momentum. Which states that the initial energy/momentum of a system is equal to the final energy/momentum. Initially, the bullet is fired and the pendulum is at rest, and finally, both the bullet and pendulum combine and start oscillating.

Complete step by step solution:
Let us first write the information given in the question.
Mass of bullet ${m_b} = 25g = 0.025kg$, the mass of the pendulum ${m_p} = 5kg$, the center of pendulum rises by a distance $h = 10cm = 0.1m$

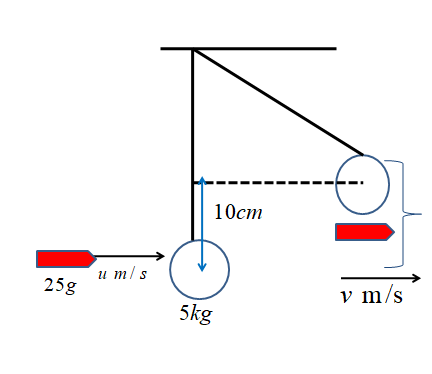
Let us use the law of conservation of momentum and also assume that the speed with which a bullet hits the pendulum is $u$and after the bullet is embedded, the speed of the system becomes $v$.
${m_p}u = ({m_p} + {m_b})v$
Let us put the values and simplify the expression.
$0.025u = (5 + 0.025)v$
$\Rightarrow u = \dfrac{{5.025}}{{0.025}}v = 201v$………………….(1)
Now to find the values of the speeds, let us also use the law of conservation of energy. That is, a change in kinetic energy is equal to a change in potential energy of the system.
$\left( {{m_p} + {m_b}} \right)gh = \dfrac{1}{2}({m_p} + {m_b}){v^2}$
Let us substitute the values in the above equation.
${v^2} = 2gh$
Let us put the values of $v$, from equation (1) in the above expression.
${\left( {\dfrac{u}{{201}}} \right)^2} = 2gh$
$\Rightarrow {u^2} = 2 \times 201 \times 201 \times 10 \times 0.1 = 80802$
$u = 284.2m/s$
Therefore, the speed of the bullet with which it strikes the pendulum is $284.2m/s$.

Note:
When one object collides with the other there are two possibilities, they will transfer energies and move with different velocities (elastic collision) or they will stick together and move with the same velocity (inelastic collision).
The sum of the potential and kinetic energy of a system is called its mechanical energy. For any system, the change in potential energy will be equal to the change in kinetic energy.