Question

A bullet of mass $10\,g$ moving horizontally with a velocity of $400\,m/s$ strikes a wooden block of mass $2\,kg$ which is suspended by a light inextensible string of length$5\,m$. As a result, the center of gravity of the block is found to rise a vertical distance of the block is found to rise a vertical distance of$10\,cm$. The speed of the bullet after it emerges out horizontally from the block will be:
A. $120\,m/s$
B. $160\,m/s$
C. $100\,m/s$
D. $80\,m/s$

Answer 1

Use the work-energy theorem to search out the horizontal velocity of the block when the bullet emerges out of it. Then use the law of conservation of momentum to search out the horizontal velocity of the bullet when it emerges out of the block.

Formula used:
Work energy theorem,
${m_2}gh = \dfrac{1}{2}{m_2}v_2^2$
The conservation of momentum
${m_1}{u_1} = {m_1}{v_1} + {m_2}{v_2}$

Complete step by step answer:
Given that, the mass of the bullet ${m_1} = 10g = 0.01kg$
Velocity${u_1} = 400m/s$
Mass of the wooden block ${m_2} = 2kg$
Length$= 5m$

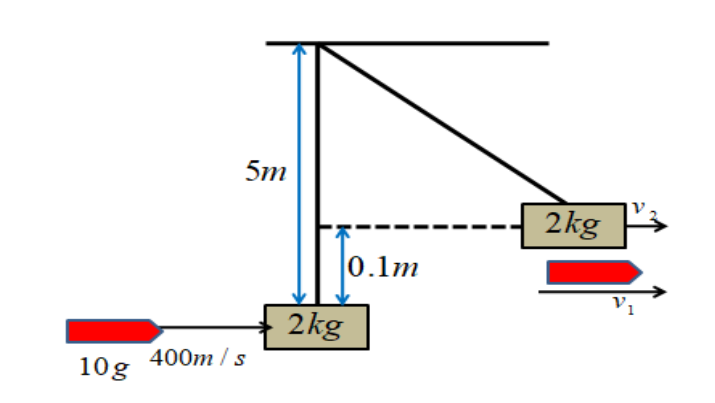
Let us consider, the velocity of the bullet and also the block after the collision will be ${v_1}$​ and ${v_2}$.​ The block rises $h = 10cm = 0.1m$. It is provided that the bullet passes through the block and we should find the horizontal velocity of the bullet when it emerges out of the block. To find this horizontal velocity, it’s also provided that after the bullet passes through the block, the block gains some momentum and, also, the center of gravity of the block rises to a height of$10cm$.

The bullet comes with some velocity and therefore strikes the block and emerges out of the block. During this process, the bullet exerts a force on the block, and also the block gains some velocity. Since the block is suspended to a string, it’ll undergo a circular motion.However, gravity will oppose its motion and after some time it comes to rest at a height of $h = 10\,cm$.

Based on the work-energy theorem, work done on a body is equal to the change in its kinetic energy,
${m_2}gh = \dfrac{1}{2}{m_2}v_2^2$
$v_2^2 = 2gh$

\Rightarrow {v_2} = \sqrt {2 \times 9.81 \times 0.1} \\\ \Rightarrow {v_2} = 1.4\,m/s$$ When the bullet passes through the block, there are only two forces performing on the system and those are the equal and opposite forces exerted by both the bodies on another.Hence, the net force on the system is zero. Therefore, we are able to use the law of conservation of momentum that says that when the net force is zero, the final and therefore the initial momentums are equal. Let $${u_1}$$​ is the initial velocity of the bullet, then according to the conservation of momentum, $${m_1}{u_1} = {m_1}{v_1} + {m_2}{v_2}$$ $$\Rightarrow {v_1} = \dfrac{{{m_1}{u_1} - {m_2}{v_2}}}{{{m_1}}} \\\ \Rightarrow {v_1} = \dfrac{{\left( {0.01 \times 400} \right) - \left( {2 \times 1.4} \right)}}{{0.01}}$$ $$\therefore {v_1} = 120\,m/s$$ Hence, the horizontal velocity of the bullet when it emerges out of the bullet is $${v_1} = 120m/s$$ **Therefore, the correct answer is option (A).** **Note:** Always remember that the units of all the physical quantities involved in the given question must be within the same system of units. Mainly, it’s the system of SI units. As an example, all the units are SI units except the units of mass of the bullet and also height.The mass of the bullet is given in grams. So we’ve to convert its unit into an SI unit i.e. kilogram$$\left( {kg} \right)$$.