Question

A bullet of mass 0.02 kg moving with a speed of $200m{{s}^{-1}}$ strikes a 2 kg wooden block suspended by a 1m long thread and is embedded in the block. What is the maximum inclination of the thread with the vertical? ($g=9.8m{{s}^{-2}}$)

Answer 1

First, use the law of conservation of linear momentum for perfectly inelastic collision and the speed of the system after the collision. Then use the work energy theorem to find the maximum height reached by the system. Later, find the maximum inclination by trigonometry.

Formula used:
Conservation of momentum for perfectly inelastic collision.
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}=({{m}_{1}}+{{m}_{2}})v$, where ${{m}_{1}},{{m}_{2}}$ are the masses of the two bodies, ${{u}_{1}},{{u}_{2}}$ are their respective initial velocities and v is the final velocity of the system.
$W=mgh$, where W is work done by gravity force when a body of mass m falls by height h and g is acceleration due to gravity.
$K=\dfrac{1}{2}m{{v}^{2}}$, where K is kinetic energy of the body moving speed v.

Complete step by step answer:
It is given that the bullet is embedded in the block. This means that when the bullet hits the block, there will be a completely inelastic collision and then the bullet and the block will travel together. Since there is no external force acting the horizontal direction, we can apply the law of conservation of momentum in that direction for perfectly inelastic collision. Here, ${{m}_{1}}=0.02kg,{{m}_{2}}=2kg,{{u}_{1}}=200m{{s}^{-1}},{{u}_{2}}=0$.

Then by applying the law of conservation of linear momentum we get that $(0.02)(200)+(2)(0)=(0.02+2)v$
$\Rightarrow v=\dfrac{2}{2.02}\\\ \Rightarrow v=\dfrac{2}{2.02}\\\ \Rightarrow v=0.99m{{s}^{-1}}$
This means that the speed of the system of the bullet and the block (of mass 2.02kg) is $0.99m{{s}^{-1}}$.Now, this system will rotate upward and the gravitational force will do a negative work on the system.Now, we shall apply the work-energy theorem, which says that total work done on a system is equal to change in its kinetic energy.
i.e. $W=\Delta K$

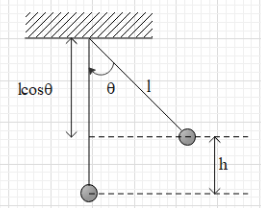
Let the maximum height reached by the system be h.
Therefore, work done by gravitational force is $W=-mgh=(2.02)(9.8)h$
(the work done by gravity is negative because the direction of the force and the displacement of the block are opposite).
$\Rightarrow W=-19.796h$ ….. (i)
The initial kinetic energy of the system is ${{K}_{1}}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}(2.02){{(0.99)}^{2}}$
$\Rightarrow {{K}_{1}}=0.9999J$
The final velocity of the block is zero. Therefore, is final kinetic energy is ${{K}_{2}}=0$
Hence, $\Delta K={{K}_{2}}-{{K}_{1}}=0-0.9999$
$\Rightarrow \Delta K=-0.9999J$ …. (ii)
Now, equate (i) and (ii).
$\Rightarrow -19.796h=-0.9999$
$\Rightarrow h=\dfrac{0.9999}{19.796}=0.05m$
From the above figure we get that $\cos \theta =\dfrac{l-h}{l}$
By substituting the values of h and l we get $\cos \theta =\dfrac{1-0.05}{1}=0.95$
$\therefore \theta ={{\cos }^{-1}}(0.95)\approx {{18.2}^{\circ }}$.

Note: If you do not know about the work energy theorem, then you can also use the law of conservation of mechanical energy since gravitational force is a conservative force.The law of conservation of mechanical energy says that the change in kinetic energy is equal to the negative of the change in potential energy of the system.