Question

A bullet of mass $0.01kg$ and travelling at a speed of $500m{s^{ - 1}}$ strikes a block of mass $2kg$ which is suspended by a string of length $5m$ . The centre of gravity of the block is found to raise a vertical distance of $0.2m$ . What is the speed of the bullet after it emerges from the block?

Answer 1

Write down the given quantities first. Draw a figure for the same. There is a rise in the centre of gravity of the block therefore energy must be conserved. Then apply conservation of linear momentum. The bullet enters and leaves the system, so the mass of the block does not increase.

Complete step by step answer:
Lets understand the question first, a block is suspended by a string. A bullet hits the block and the centre of gravity of the block increases. Simultaneously the bullet emerges out of the block. We have to find the speed of the bullet as it emerges out.Lets first draw the figure for the same:

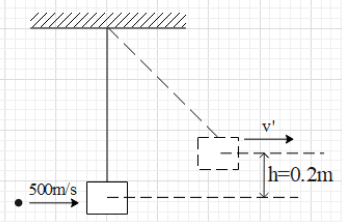
The grey lines are used to indicate the change in center of mass of the block. Please note that the bullet hits from the left end and emerges out from the right end.Let’s write the given quantities:
Mass of block ${m_{block}} = 2kg$
Mass of bullet ${m_{bullet}} = 0.1kg$
Initial speed of bullet ${u_b} = 500m{s^{ - 1}}$
Initial speed of block ${u_{block}} = 0$
Rise in centre of mass of block $h = 0.2m$
The energy of the system is conserved:
Loss of kinetic energy must be equal to the gain in potential energy
The initial kinetic energy of the block was zero and finally the block will gain some velocity as well as potential energy.
$\dfrac{1}{2}m{v^2} - 0 = mgh$
$\Rightarrow v = \sqrt {2gh}$
$\Rightarrow v = \sqrt {2 \times 10 \times 0.2}$
$\Rightarrow v = 2m{s^{ - 1}}$
This will be the velocity of the block.
For the velocity of the bullet, since no external force is acting on the system, therefore its momentum must be conserved:
${m_{bullet}} \times {u_b} + {m_{block}} \times {u_{block}} = {m_{bullet}} \times {v^1} + {m_{block}} \times {v_{block}}^1$
$\Rightarrow 0.01 \times 500 + 2 \times 0 = 0.01 \times {v^1} + 2 \times 2$
$\Rightarrow 0.01{v^1} = 1$
$\therefore {v^1} = 100m{s^{ - 1}}$

Therefore, the speed of the bullet after it emerges from the block is $100m{s^{ - 1}}$.

Note: Remember that when no external force is acting on a system, the momentum of the system is conserved. Here, the block gains kinetic energy as well as potential energy.Do remember that energy of the system is always conserved unless any loss is mentioned.