Question

A bullet fired into a wooden block loses half of its velocity after penetrating $40cm$. It comes to rest after penetrating a further distance given as,
$\begin{aligned} & A.\dfrac{22}{3}cm \\\ & B.\dfrac{40}{3}cm \\\ & C.\dfrac{20}{3}cm \\\ & D.\dfrac{22}{5}cm \\\ \end{aligned}$

Answer 1

First of all find out the acceleration by the use of the third equation of motion. The velocities and distance travelled as mentioned in the question. After that find out the distance traversed by the same bullet after $40cm$. Here also uses Newton's third equation of motion. Substitute the value of acceleration obtained before and rearrange the equation in terms of distance of penetration.

Complete answer:
Let us assume that the initial velocity of the bullet be $V$,

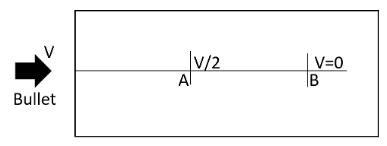
The distance of penetration of the bullet when it enters is mentioned as $40cm$.
Therefore when the bullet penetrates $0.4m$, then we can write the final velocity of this journey as,
$0.4m=\dfrac{V}{2}$
Applying the newton’s third law of motion,
${{V}^{2}}={{U}^{2}}+2as$
Substituting the values in it will give,
${{\left( \dfrac{V}{2} \right)}^{2}}={{V}^{2}}-2a\left( 0.4 \right)$
Here the acceleration will be negative since the body is about to be at rest. That is the body is decelerating.
Rearranging the above given equation will be given as,
$\dfrac{{{\left( \dfrac{V}{2} \right)}^{2}}-{{V}^{2}}}{2\times \left( 0.4 \right)}=a$
That is,
$\dfrac{3{{V}^{2}}}{4\times \left( 0.8 \right)}=a$
Now let us look at the journey of a bullet after $40cm$.
Here we can write that,
According to newton’s equation of motion,
$0=\dfrac{{{V}^{2}}}{4}-2a\left( x \right)$
Where $x$ be the distance up to which the bullet penetrates.
As the bullet is coming to rest the final velocity will be zero.
This equation can be rewritten as,
$\dfrac{{{V}^{2}}}{4}=2a\left( x \right)$
Now let us substitute the value of deceleration in this equation,
$\dfrac{{{V}^{2}}}{4}=2\times \dfrac{3{{V}^{2}}}{4\times \left( 0.8 \right)}\times \left( x \right)$
Now let us cancel out all the common terms from the equation,
$1=\dfrac{6}{\left( 0.8 \right)}\times \left( x \right)$
Rearranging the equation in terms of the distance penetrated will be given as,
$\dfrac{0.8}{6}=x$
$x=\dfrac{0.4m}{3}=\dfrac{40}{3}cm$

So, the correct answer is “Option B”.

Note:
Acceleration of a body is given as the change in velocity with respect to time. This means that the body will get the velocity increased in every interval of time. Uniform acceleration is when the velocity increases regularly as the time increases. Deceleration means the velocity decreases as the time increases.