Question

A bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?

• A. 1.5 cm
• B. 1.0 cm
• C. 3.0 cm
• D. 2.0 cm

Answer 1

Answer: (B)

1.0 cm

Answer 2

Let initial velocity of the bullet = u

After penetrating 3 cm its velocity becomes $\frac{u}{2}$

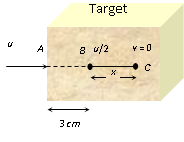
From $v^{2} = u^{2} - 2as$ $\left( \frac{u}{2} \right)^{2} = u^{2} - 2a(3)$

⇒ $6a = \frac{3u^{2}}{4}$ ⇒ $a = \frac{u^{2}}{8}$

Let further it will penetrate through distance x and stops at point C.

For distance BC, $v = 0,u = u/2,s = x,a = u^{2}/8$

From $v^{2} = u^{2} - 2as$⇒$0 = \left( \frac{u}{2} \right)^{2} - 2\left( \frac{u^{2}}{8} \right).x$ ⇒$x = 1$ cm.