Question
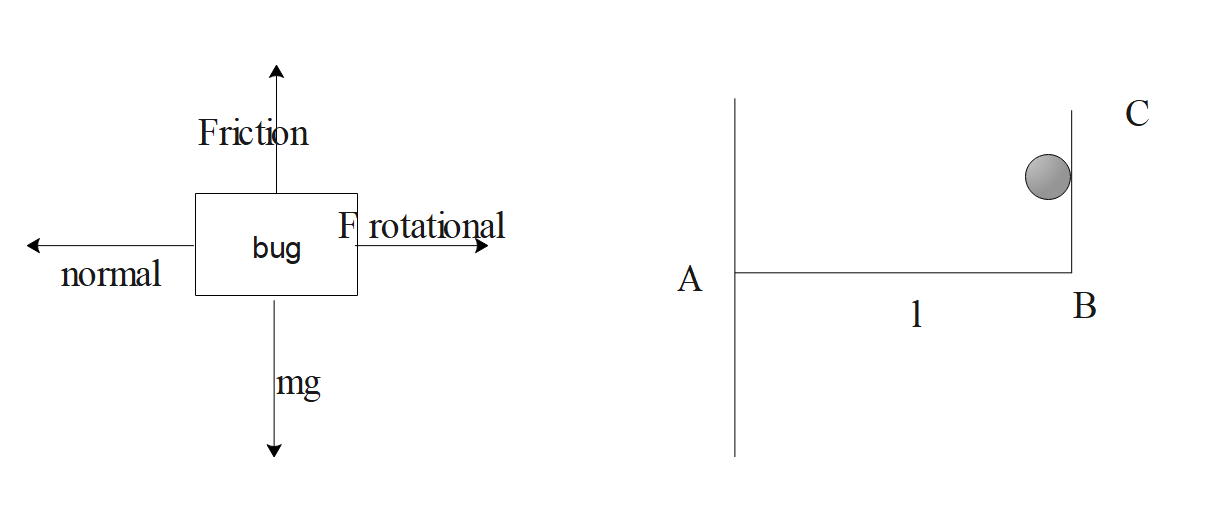
Question: A bug rests on vertical part bc of frame ABC. Frame rotates with constant velocity. Length of the pa...
A bug rests on vertical part bc of frame ABC. Frame rotates with constant velocity. Length of the part ab is l. Minimum value of coefficient of friction between wire and bug for bug not to fall must be,
Solution
Let us first draw a free body diagram of the bug on the vertical part of the frame ABC. Write the net forces acting on the bug when the frame is rotated with angular velocity. As net force acting outside the frame is zero, equal the horizontal and vertical forces.
Complete answer:
Let us note the forces acting on the bug when the frame rotates with angular velocity. Normal acts towards the negative x axis, rotational force acts outwards, means positive x axis. Frictional force acts in the positive y axis and the force due to gravitation will act in the negative y axis respectively.
Let us check the free body diagram of the bug,
We will get the following forces in horizontal and vertical directions,
N=mω2l⇒μN=mg⇒μ(mω2l)=mg⇒μ=ω2lg
Additional Information:
Angular velocity is the rate of change of the angle in certain time. It is analogous to linear velocity. The relation between the linear velocity and angular velocity is that linear velocity is the radius times the angular velocity. In daily times, we can use this application like, a larger tire radius rotating at the same angular velocity will be producing a larger linear speed for the car eventually. In general, we measure the angular velocity in angle per unit time. For example, for satellites, we use radians per second as the unit to measure the angular velocity. Rotating around a fixed axis or about a fixed axis of revolution or motion with respect to fixed axis of rotation is a special case of rotational motion. The fixed axis hypothesis excludes the possibility of an axis changing its orientation and also it cannot describe natural procedures like wobbling or precession.
Note:
The normal of the bug is taken in a horizontal direction because the bud is holding the rod in vertical position. The gravitational force causes the bug to fall down gradually.as there’s some amount of rotational force acting on the bug, all these forces result in the bug not falling down easily.
