Question

A bucket contains water filled up to height $= 15\;cm$. The bucket is tied to a rope, which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above the atmospheric pressure at the bottom is:
A). $0.5\;kPa$
B). $1\;kPa$
C). $5\;kPa$
D). None of these

Answer 1

First find the effective gravitational acceleration keeping in mind both the water pressure as well as atmospheric pressure. In other words, using free-body diagrams, one for the bucket and one for the weight, first, find the acceleration ‘a’ due to the pulley f in terms of g, and then find the effective acceleration due to gravity (g-a). To this end, try and recall the relation for fluid pressure at depth in terms of height and density of a fluid and g.

Formula Used:
Fluid pressure at a depth: $P = d\rho g_{eff}$, where d is the depth, $\rho$ is the density of the fluid, and $g_{eff}$ is the effective acceleration due to gravity after accounting for both fluid pressure and atmospheric pressure.

Complete step-by-step solution:
__
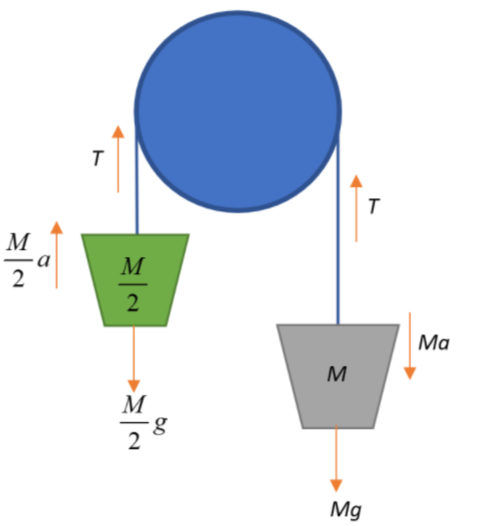
Let us deconstruct the question and deduce some inferences that will facilitate our calculation.
In our pulley system, on one end, we have a bucket of water that is filled up to height is $h = 15\;cm$, and has a mass of $M$.
On the other end, we have suspended the weight of mass $\dfrac{M}{2}$.
Let us analyze the forces acting on the weight and the bucket.
For the bucket:
$T- Ma = Mg \Rightarrow T = Mg - Ma$
where T is the tension in the rope, g is the acceleration due to gravity and a is the linear acceleration produced by the movement of the rope over the pulley.
For the weight:
$T- \dfrac{M}{2}g = \dfrac{M}{2}a \Rightarrow T = \dfrac{M}{2}g + \dfrac{M}{2}a$
Equating the above two equations, we get:
$Mg - Ma = \dfrac{M}{2}g + \dfrac{M}{2}a \Rightarrow g - a = \dfrac{g}{2} + \dfrac{a}{2} \Rightarrow \dfrac{a}{2}+a = g- \dfrac{g}{2}$
$\Rightarrow \dfrac{3a}{2} = \dfrac{g}{2} \Rightarrow a = \dfrac{g}{3}$
Therefore the effective acceleration acting on the water filled bucket will be : $g-a = g-\dfrac{g}{3} = \dfrac{2g}{3}$.
Since we are expressing it in terms of g, we can call it the effective acceleration due to gravity, hence, $g_{eff} = \dfrac{2g}{3}$.
Therefore, the effective pressure at the bottom of the water filled bucket:
$\rho_{water} = 1000 kgm^{-3}$
$P = h\rho g_{eff} = 0.15 \times 1000 \times \dfrac{2 \times 9.8}{3} = 0.98 \times 10^3\; Pa \approx 1\;kPa$
Therefore, the correct choice would be: B. $1\;kPa$

Note: Remember to discount the atmospheric pressure in the final pressure calculation since the question asks for us to find only the water pressure above the atmospheric pressure at the bottom of the bucket.
The final relation that we used for pressure can be derived as follows:
Pressure $P = \dfrac{Force}{Area} = \dfrac{mg}{A}$
Mass of the fluid $m = density \times volume = \rho V$
Volume of the fluid $V = area \times height = Ah$
Therefore mass $m = \rho Ah$
Hence Pressure $P = \dfrac{(\rho Ah)g}{A} = h\rho g$
If the fluid is accelerating with acceleration a, then,
Pressure $P = h\rho g - h\rho a = h\rho (g -a) = h\rho g_{eff}$