Question
Question: A bubble having surface tension T and radius R is formed on a ring of radius b(b < < R). Air is blow...
A bubble having surface tension T and radius R is formed on a ring of radius b(b < < R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. What is the radius at which the bubble separates from the ring?
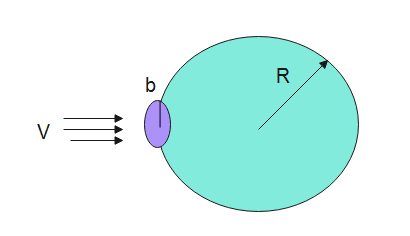
Solution
In this question, we use the relations between the pressure, temperature, force and area. Further we will deduce a relation to find the density using these expressions. Further, we will relate the relation between density and the radius, which will give us the required result.
Formula used:
p=R4T
F=R4TA
F1=ρAv2
Complete step by step solution:
as we know that the surface tension on any liquid is defined as the attractive force in liquids that pulls the surface molecules into the rest of the liquid, thereby, minimizing the surface area. These attractive forces are due to electrostatic forces.
Excess pressure inside a bubble is given as:
p=R4T
Let area of bubble at wall where airstrikes be A. So, the force due to excess pressure will be given as:
F=R4TA
Here, the force due to striking air will be given as:
F1=ρAv2
Now, from above equation we get:
\eqalign{ & \rho A{v^2} = \dfrac{{4TA}}{R} \cr
& \therefore R = \dfrac{{4T}}{{\rho {v^2}}} \cr}
Therefore, the radius at which the bubble separates from the ring is given by the above equation R.
Additional Information: From the law of conservation of mass which says that mass can neither be created nor destroyed in any chemical reactions. Also, it can be defined as the mass of any one element at the beginning of a reaction will equal the mass of that element at the end of the reaction.
We know that collision means when two objects come in contact with each other for a very short period. Collision is an interaction between two masses for a very short interval where the momentum and energy of the colliding masses changes. Here are two types of collision: first id elastic collision where the energy remains same after interaction or collision and second is inelastic collision where the final energy changes after the collision of the particles or body.
Note: We should remember that the surface tension depends on the force and the length of the object. Also, density is given as ratio of mass and volume, which means that when mass increases the density also increases, whereas when the volume increases the density decreases.
