Question

A bridge over a railway track is in the form of a circular arc of radius $55\,{\text{m}}$. What is the limiting speed with which a car can cross the bridge so that no contact is lost if the centre of gravity of the car is $0.4\,{\text{m}}$ above the road? (in m/s)
A. 28.3
B. 24.3
C. 25.3
D. 23.3

Answer 1

Determine the balanced equation of forces on the car using Newton’s second law of motion. Determine the radius of the circular arc for the car considering the distance of centre of gravity from the road. Derive the equation for the limiting speed of the car for which no contact is lost between the road and the car.

Formula used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is the net force on the object, $m$ is the mass of the object and $a$ is the acceleration of the object.
The expression for the centripetal force ${F_C}$ is
${F_C} = \dfrac{{m{v^2}}}{R}$ …… (2)
Here, $m$ is the mass of the object, $v$ is the velocity of the object and $R$ is the radius of the circular path.

Complete step by step answer:
The car travels on a bridge of circular arc shape with radius $55\,{\text{m}}$
$r = 55\,{\text{m}}$.
But the centre of gravity of the car is $0.4\,{\text{m}}$ above the road.
Hence, the radius of the circular track is the sum of $55\,{\text{m}}$ and $0.4\,{\text{m}}$.
$R = \left( {55\,{\text{m}}} \right) + \left( {0.4\,{\text{m}}} \right)$
$\Rightarrow R = 55.4\,{\text{m}}$
Hence, the radius of the circular track for the car becomes $55.4\,{\text{m}}$.
The free body diagram of the car is as follows:

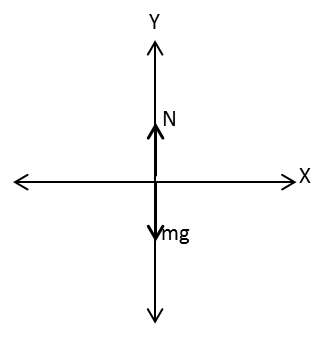
The weight $mg$ of the car acts in the downward direction and the normal force $N$ exerted by the bridge on the car is in the upward direction.
At the top of the bridge, the car is in equilibrium with its limiting speed.
The two forces weight of the car and normal force on the car by the bridge together provides the centripetal force to the car.
$mg + N = {F_C}$
Substitute $\dfrac{{m{v^2}}}{R}$ for ${F_C}$ in the above equation.
$mg + N = \dfrac{{m{v^2}}}{R}$
As the car loses contact with the bridge, the normal force exerted by the bridge on the car becomes zero and the velocity becomes the limiting speed.
Substitute $0\,{\text{N}}$ for $N$ in the above equation.
$mg + \left( {0\,{\text{N}}} \right) = \dfrac{{m{v^2}}}{R}$
$\Rightarrow mg = \dfrac{{m{v^2}}}{R}$
$\Rightarrow v = \sqrt {Rg}$
Substitute $55.4\,{\text{m}}$ for $R$ and $9.8\,{\text{m/}}{{\text{s}}^2}$ for $g$ in the above equation.
$\Rightarrow v = \sqrt {\left( {55.4\,{\text{m}}} \right)\left( {9.8\,{\text{m/}}{{\text{s}}^2}} \right)}$
$\therefore v = 23.3\,{\text{m/s}}$

Therefore, the limiting speed of the car is $23.3\,{\text{m/s}}$.

So, the correct answer is “Option D”.

Note:
One can directly use the equation for the limiting speed without deriving it as the equation is already proved in many cases before.
The limiting speed of the car for which no contact is lost between the road and the car.