Question

A bridge over a canal is in the form of circular arc of radius $5m$. The maximum speed with which a motorcycle crosses the bridge without leaving the ground at the highest point is $g = 10m{s^{ - 2}}$
$\left( {\text{A}} \right){\text{ }}10{\text{m}}{{\text{s}}^{ - 2}}$
$\left( {\text{B}} \right){\text{ }}50{\text{m}}{{\text{s}}^{ - 2}}$
$\left( {\text{C}} \right){\text{ }}100{\text{m}}{{\text{s}}^{ - 2}}$
$\left( {\text{D}} \right){\text{ }}5\sqrt 2 {\text{m}}{{\text{s}}^{ - 2}}$

Answer 1

First we discuss the variation of position in the different axis and also, the direction and the magnitude of tangential velocity of the particle. Then we use the formula and put the given values in it. On some simplification we get the required answer.

Formula used:
$\dfrac{{{{\text{v}}^2}}}{{\text{r}}} = {\text{g}}$, here $v =$ speed, $r =$ radius of the circular arc.

Complete step by step answer:

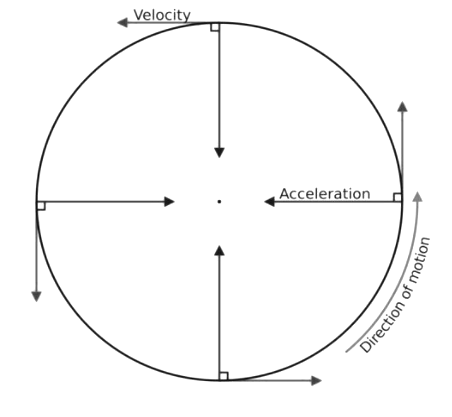
• Change in position of the particle along the X-axis: The uniform circular motion can take place in any coordinate, it’s not necessary to accelerate in a particular direction (as said in X-axis).
• Change in position of the particle along the Y-axis: The uniform circular motion can take place in any coordinate; it's not necessary to accelerate in a particular direction (as said in the Y-axis).
• Change in direction of tangential velocity: The direction of the velocity keeps on changing continuously along with time.
• Change in the magnitude of tangential velocity: In a uniform circular motion, the radial velocity is always constant so the magnitude of the velocity remains unchanged throughout the circular motion.

Therefore, by using the equation, we get, $\dfrac{{{{\text{v}}^2}}}{{\text{r}}} = {\text{g}}$
Taking cross multiplication and we get,
$\Rightarrow {{\text{v}}^2}{\text{ = rg}}$
On squaring on both sides we get,
$\Rightarrow {\text{v = }}\sqrt {{\text{rg}}}$
Now, substituting the values we get,
$\Rightarrow {\text{v = }}\sqrt {5 \times 10}$
On splitting the values and we get,
$\Rightarrow {\text{v = }}\sqrt {5 \times 2 \times 5}$
On multiplication we get,
$\Rightarrow {\text{v = }}\sqrt {25 \times 2}$
Taking the root value and we get,
$\Rightarrow {\text{v = 5}}\sqrt 2 {\text{m}}{{\text{s}}^{ - 2}}$

Hence, the correct answer is option (D).

Note: Uniform circular motion is defined as the motion of a particle (small body) along a circular path in which the speed remains constant but the velocity may change due to the change in direction of the velocity continuously.
At each position, the velocity vector is perpendicular to the radius vector.
The angular displacement of a particle moving in a circular path is the angle swept out by its radius vector in the given time interval measured in radian.
The rate of change of angular displacement of a particle is called angular velocity measured in $radian/sec$.
The time rate of change of angular velocity of a particle is called its angular acceleration measured in $radian/sec^2$.