Question

A brick with dimensions of $20cm\times 10cm\times5 cm$ has a weight $500gwt$. Calculate the pressure exerted by it when it rests on different faces.

& \text{A}\text{. Case i) }{{\text{P}}_{1}}=1.25g/c{{m}^{2}},Case\text{ ii)}{{\text{P}}_{2}}=5g/c{{m}^{2}},\text{ Case iii)}{{\text{P}}_{3}}=5g/c{{m}^{2}} \\\ & \text{B}\text{. Case i) }{{\text{P}}_{1}}=2.5g/c{{m}^{2}},Case\text{ ii)}{{\text{P}}_{2}}=5g/c{{m}^{2}},\text{ Case iii)}{{\text{P}}_{3}}=10g/c{{m}^{2}} \\\ & \text{C}\text{. Case i) }{{\text{P}}_{1}}=5g/c{{m}^{2}},Case\text{ ii)}{{\text{P}}_{2}}=25g/c{{m}^{2}},\text{ Case iii)}{{\text{P}}_{3}}=15g/c{{m}^{2}} \\\ & \text{D}\text{. Case i) }{{\text{P}}_{1}}=2.5g/c{{m}^{2}},Case\text{ ii)}{{\text{P}}_{2}}=2.5g/c{{m}^{2}},\text{ Case iii)}{{\text{P}}_{3}}=10g/c{{m}^{2}} \\\ \end{aligned}$$

Answer 1

We know that pressure is the thrust applied per unit area of the surface. Here we have the dimensions of the brick which in turn will give the surfaces of the brick. Also the weight of the brick is given hence we can calculate the force.

Formula used:
$P=\dfrac{T}{A}$

Complete step by step answer:
We know that a brick is a cuboid. We also know that a cuboid has $6$ faces or $3$ pairs of rectangular faces. The dimensions of the cuboid are given as $20cm\times 10cm\times5 cm$ and is as shown below

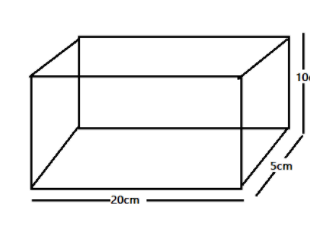
Also the mass of the brick is given as $m=500g$, which is also the thrust $T$ due to the brick.
Since the faces are rectangular, we know that their area is given as $l\times b$ where $l$ is the length and $b$ is the breadth of the rectangle.
Let us assume, $P_{1}$ to be the pressure on the surface $1$ whose dimension is given by $20cm\times 10cm$
Then the area of the surface is given as $A_{1}=20cm\times 10cm=200cm^{2}$
Then, $P_{1}=\dfrac{500}{200}=2.5g/cm^{2}$
Let us assume $P_{2}$, to be the pressure on the surface $2$ whose dimensions is given by $20cm\times 5cm$
Then the area of the surface is given as $A_{2}=20cm\times 5cm=100cm^{2}$
Then $P_{2}=\dfrac{500}{100}=5g/cm^{2}$

Let us assume $P_{3}$, to be the pressure on the surface $3$ whose dimension is given by $10cm\times 5cm$
Then the area of the surface is given as $A_{3}=10cm\times 5cm=50cm^{2}$
Then $P_{3}=\dfrac{500}{50}=10g/cm^{2}$
Hence the answer is $\text{B}\text{. Case i) }{{\text{P}}_{1}}=2.5g/c{{m}^{2}},Case\text{ ii)}{{\text{P}}_{2}}=5g/c{{m}^{2}},\text{ Case iii)}{{\text{P}}_{3}}=10g/c{{m}^{2}}$

Note:
One may assume surface $3$ as surface $2$ or surface $1$ also. It doesn’t matter. The values of the pressure may get interchanged with respect to the order in which the dimensions are taken. Hence don’t expect the values to be in the same order as given in the options.